题目内容
3.已知点A(a,0)和点B(0,5),且直线AB与坐标轴围成的△AOB的面积等于10,则a的值是4或-4.分析 根据三角形面积公式得到$\frac{1}{2}$×5×|a|=10,然后解绝对值方程即可.
解答 解:根据题意得$\frac{1}{2}$×5×|a|=10,
解得a=4或a=-4.
故答案为4或-4.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
14.下列各组x、y的值,是二元一次方程x-y=5的一个解的是( )
| A. | $\left\{\begin{array}{l}x=-1\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=4\end{array}\right.$ |
18.下列说法中正确的是( )
| A. | 36的平方根是6 | B. | 8的立方根是2 | ||
| C. | $\sqrt{4}$的平方根是±2 | D. | 9的算术平方根是-3 |
13.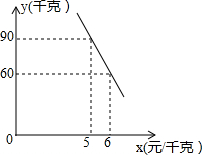 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.(1)根据题意,填写如表:
| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
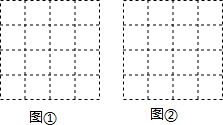 如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.
如图,正方形网格中每个小正方形的边长都是1,每个小格的格点叫做“格点”,以格点为顶点分别按下列要求画出三角形.