题目内容
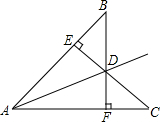 如图,已知:BF⊥AC,CE⊥AB,垂足分别是F、E,BF、CE交于点D.若BD=CD,请问:AD平分∠BAC吗?若AD平分∠BAC,请给出证明;若AD不平分∠BAC,请说明理由.
如图,已知:BF⊥AC,CE⊥AB,垂足分别是F、E,BF、CE交于点D.若BD=CD,请问:AD平分∠BAC吗?若AD平分∠BAC,请给出证明;若AD不平分∠BAC,请说明理由.分析:首先利用全等三角形的判定得出△BDE≌△CDF,即可得出DE=DF,再利用角平分线的性质得出即可.
解答:解:∵BF⊥AC,CE⊥AB,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中
,
∴△BDE≌△CDF(AAS),
∴DE=DF,
又∵BF⊥AC,CE⊥AB,
∴D点在∠BAC的角平分线上,
∴∠EAD=∠FAD.
∴∠BED=∠CFD=90°,
在△BDE和△CDF中
|
∴△BDE≌△CDF(AAS),
∴DE=DF,
又∵BF⊥AC,CE⊥AB,
∴D点在∠BAC的角平分线上,
∴∠EAD=∠FAD.
点评:此题主要考查了全等三角形的判定与性质以及角平分线的判定与性质,根据已知得出DE=DF是解题关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 6、如图,已知EC=BF,∠A=∠D,现有下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;从中选取一个条件,以保证△ABC≌△DEF,则可选择的有( )
6、如图,已知EC=BF,∠A=∠D,现有下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;从中选取一个条件,以保证△ABC≌△DEF,则可选择的有( ) 11、如图,已知AE∥BF,∠E=∠F,要使△ADE≌△BCF,可添加的条件是
11、如图,已知AE∥BF,∠E=∠F,要使△ADE≌△BCF,可添加的条件是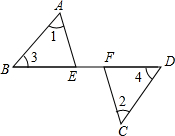 如图,已知:BF=DE,∠1=2,∠3=∠4,求证:AE=CF.
如图,已知:BF=DE,∠1=2,∠3=∠4,求证:AE=CF.