Question

【题目】在中，，是边上不同于、的一动点，过作，垂足为，连接．

试说明不论点在边上何处时，都有与相似；

若，，当为何值时，面积最大，并求出最大值；

在中，两条直角边、满足关系式，是否存在一个的值，使既与全等，也与全等．

Answer 1

【答案】见解析；当时，的面积最大，最大值是；存在．时，既与全等，也与全等．

【解析】

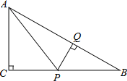
(1)无论P点如何运动，∠B为公共角，且∠PQB=∠ACB=90°，故两三角形恒相似；

(2)设，由可用含x的表达式分别表示PQ和AQ，再利用面积公式列出的表达式进行求解即可；

(3)由可得，由可得，在RT△ABC中运用勾股定理即可求解.

不论点在边上何处时，都有

，

∴；

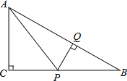
设，由勾股定理，得

∵由知，，

∴，即

∴，

∴当时，的面积最大，最大值是；

存在．

∵

∴

又∵

∴

∴

在中，由勾股定理得

∴

∴时，既与全等，也与全等．