题目内容
 如图,直角坐标系中,点A(2,2)在反比例函数y=
如图,直角坐标系中,点A(2,2)在反比例函数y=| k1 |
| x |
| k2 |
| x |
| AB |
| BC |
| 4 |
| 3 |
(1)k2的值为
(2)点P(0,a)是y轴上一点,连结PA.将线段PA绕点P按逆时针方向旋转90°,所得的像为PA′.若PA′与反比例函数y=
| k1 |
| x |
| k2 |
| x |
考点:反比例函数综合题
专题:分类讨论
分析:(1)由条件易求出点C的坐标,然后用待定系数法就可解决问题.
(2)根据点A′相对于y轴的不同位置进行讨论,通过三角形全等求出点A′的坐标,然后考虑点A′刚好落到反比例函数图象上时对应的a的值,就可求出a的取值范围.
(2)根据点A′相对于y轴的不同位置进行讨论,通过三角形全等求出点A′的坐标,然后考虑点A′刚好落到反比例函数图象上时对应的a的值,就可求出a的取值范围.
解答:解:(1)如图1,
∵点A(2,2),∴AB=2.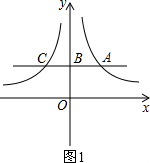
∵
=
,∴BC=
.
∴点C的坐标为(-
,2).
∵点C(-
,2)在反比例函数y=
(x<0)图象上,
∴k2=-
×2=-3.
故答案为:-3.
(2)①当点A′在y轴的右侧时,
此时a>2.
过点A′作A′E⊥OB于E,如图2.
∵AB⊥OB,A′E⊥OB,∠APA′=90°,
∴∠ABP=∠A′EP=∠APA′=90°.
∴∠APB=90°-∠A′PE=∠EA′P.
在△ABP和△PEA′中,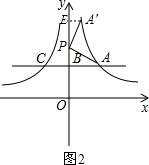
.
∴△ABP≌△PEA′.
∴AB=PE,BP=EA′.
∵A(2,2),P(0,a),
∴PE=AB=2,EA′=BP=a-2.
∴OE=OP+PE=a+2.
∴点A′的坐标为(a-2,a+2).
当A′(a-2,a+2)在反比例函数y=
(x>0)的图象上时,如图2.
∵A(2,2)在反比例函数y=
(x>0)的图象上,
∴k1=2×2=4.
∴(a-2)(a+2)=4.
解得:a=±2
.
∵a>2,∴a=2
.
②当点A′在y轴上时,
此时a=2,点A′与两函数的图象没有交点,故舍去.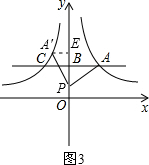
③当点A′在y轴的左侧时,
此时a<2.
Ⅰ.0≤a<2,
当A′(a-2,a+2)在反比例函数y=-
(x<0)的图象上时,
过点A′作A′E⊥OB于E,如图3.
同理可得:A′的坐标为(a-2,a+2).
∵A′(a-2,a+2)在反比例函数y=-
(x<0)的图象上,
∴(a-2)(a+2)=-3.
解得:a=±1.
∵0≤a<2,∴a=1.
Ⅱ.a<0,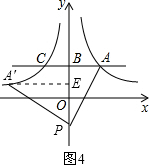
当A′(a-2,a+2)在反比例函数y=-
(x<0)的图象上时,
过点A′作A′E⊥OB于E,如图4.
同理可得:A′的坐标为(a-2,a+2).
∵A′(a-2,a+2)在反比例函数y=-
(x<0)的图象上,
∴(a-2)(a+2)=-3.
解得:a=±1.
∵a<0,∴a=-1.
综上所述:符合要求的a的取值范围是a≥2
或-1≤a≤1.
故答案为:a≥2
或-1≤a≤1.
∵点A(2,2),∴AB=2.

∵
| AB |
| BC |
| 4 |
| 3 |
| 3 |
| 2 |
∴点C的坐标为(-
| 3 |
| 2 |
∵点C(-
| 3 |
| 2 |
| k2 |
| x |
∴k2=-
| 3 |
| 2 |
故答案为:-3.
(2)①当点A′在y轴的右侧时,
此时a>2.
过点A′作A′E⊥OB于E,如图2.
∵AB⊥OB,A′E⊥OB,∠APA′=90°,
∴∠ABP=∠A′EP=∠APA′=90°.
∴∠APB=90°-∠A′PE=∠EA′P.
在△ABP和△PEA′中,

|
∴△ABP≌△PEA′.
∴AB=PE,BP=EA′.
∵A(2,2),P(0,a),
∴PE=AB=2,EA′=BP=a-2.
∴OE=OP+PE=a+2.
∴点A′的坐标为(a-2,a+2).
当A′(a-2,a+2)在反比例函数y=
| k1 |
| x |
∵A(2,2)在反比例函数y=
| k1 |
| x |
∴k1=2×2=4.
∴(a-2)(a+2)=4.
解得:a=±2
| 2 |
∵a>2,∴a=2
| 2 |
②当点A′在y轴上时,
此时a=2,点A′与两函数的图象没有交点,故舍去.

③当点A′在y轴的左侧时,
此时a<2.
Ⅰ.0≤a<2,
当A′(a-2,a+2)在反比例函数y=-
| 3 |
| x |
过点A′作A′E⊥OB于E,如图3.
同理可得:A′的坐标为(a-2,a+2).
∵A′(a-2,a+2)在反比例函数y=-
| 3 |
| x |
∴(a-2)(a+2)=-3.
解得:a=±1.
∵0≤a<2,∴a=1.
Ⅱ.a<0,

当A′(a-2,a+2)在反比例函数y=-
| 3 |
| x |
过点A′作A′E⊥OB于E,如图4.
同理可得:A′的坐标为(a-2,a+2).
∵A′(a-2,a+2)在反比例函数y=-
| 3 |
| x |
∴(a-2)(a+2)=-3.
解得:a=±1.
∵a<0,∴a=-1.
综上所述:符合要求的a的取值范围是a≥2
| 2 |
故答案为:a≥2
| 2 |
点评:本题考查了用待定系数法求反比例函数的解析式、反比例函数图象上点的坐标特征、全等三角形的判定与性质等知识,考查了分类讨论的数学思想,而合理分类及考虑临界位置是解决本题的关键.

练习册系列答案
相关题目
下列等式从左到右的变形是因式分解的是( )
| A、15a3b=3a2•5ab |
| B、(a+3)(a-3)=a2-9 |
| C、-4x2+4xy-y2=-(2x-y)2 |
| D、4x2+8x-1=4x(x+2)-1 |
 如图.∠AOB内有三条射线OC、OD、OE,则图中共有
如图.∠AOB内有三条射线OC、OD、OE,则图中共有