题目内容
8．先化简，再求值：（x-4+$\frac{9}{x+2}$）÷$\frac{{（x-1）}^{2}}{{x}^{2}-4}$，其中x的值从$\left\{\begin{array}{l}{-x＜2}\\{2x-1≤4}\end{array}\right.$的整数解中选取一个．分析 根据分式的除法和加法可以化简题目中的式子，然后在$\left\{\begin{array}{l}{-x＜2}\\{2x-1≤4}\end{array}\right.$的解集中选取一个使得原分式有意义的x的值代入即可解答本题．
解答 解：（x-4+$\frac{9}{x+2}$）÷$\frac{{（x-1）}^{2}}{{x}^{2}-4}$
=$\frac{（x-4）（x+2）+9}{x+2}•\frac{（x+2）（x-2）}{（x-1）^{2}}$
=$\frac{{x}^{2}-2x+1}{x+2}•\frac{（x+2）（x-2）}{（x-1）^{2}}$
=$\frac{（x-1）^{2}}{x+2}•\frac{（x+2）（x-2）}{（x-1）^{2}}$
=x-2，
由$\left\{\begin{array}{l}{-x＜2}\\{2x-1≤4}\end{array}\right.$得，-2＜x≤2.5，
∴当x=0时，原式=0-2=-2．
点评 本题考查分式的化简求值、一元一次不等式的整数解，解答本题的关键分式化简求值的方法，利用不等式的性质解答．
练习册系列答案
相关题目
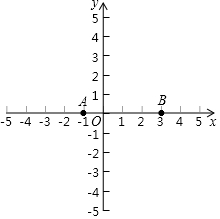如图，在平面直角坐标系xOy中，抛物线y=-x2+bx+c经过A（-1，0），B（3，0）两点．
如图，在反比例函数图象中，△AOB是等边三角形，点A在双曲线的一支上，将△AOB绕点O顺时针旋转α（0°＜α＜180°），使点A仍在双曲线上，则α=30°．