题目内容
18.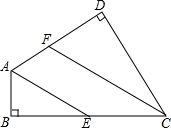 如图,已知四边形ABCD中,∠D=∠B=90°.
如图,已知四边形ABCD中,∠D=∠B=90°.(1)填空:∠DAB+∠BCD=180°;
(2)若AE平分∠DAB,CE平分∠BCD,求证:AE∥CF.
分析 (1)根据四边形的内角和解答即可;
(2)根据由平行线的性质可得到∠DFC=∠FAE,结合角平分线的定义和已知条件可求得∠DCF=∠BAE,可求得∠DCF=∠BEA=∠FCB,可证得结论.
解答 解:(1)∵四边形ABCD中,∠D=∠B=90°,
∴∠DAB+∠BCD=360°-90°-90°=180°,
故答案为:180;
(2)∵AE平分∠DAB,CF平分∠BCD
∴∠DAE=$\frac{1}{2}$∠DAB,∠DCF=$\frac{1}{2}$∠DCB,
∴∠DAE+∠DCF=$\frac{1}{2}$∠DAB+$\frac{1}{2}$∠DCB=$\frac{1}{2}$(∠DAB+∠DCB),
由(1)得:∠DAB+∠DCB=180°
∴∠DAE+∠DCF=90°,
∵∠D=90°,
∴∠DFC+∠DCF=90°,
∴∠DAE=∠DFC,
∴AE∥CF.
点评 本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
6.已知a=(-1)2016,b=-(-1.2),c=-32,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | b>a>c |
10.下表给出了二次函数y=-x2+bx+c中两个变量y与x的一些对应值:
(1)根据表格中的数据,确定b,c,n的值;
(2)直接写出抛物线y=-x2+bx+c的顶点坐标和对称轴;
(3)当y>0时,求自变量x的取值范围.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 5 | n | c | 2 | -3 | -10 | … |
(2)直接写出抛物线y=-x2+bx+c的顶点坐标和对称轴;
(3)当y>0时,求自变量x的取值范围.
 如图,直线AB、CD相交于点O,∠AOC+∠BOD=210°,则∠BOC=75°.
如图,直线AB、CD相交于点O,∠AOC+∠BOD=210°,则∠BOC=75°. 如图,这是一个由5个正方体组成的立体图形,从上面看得到的平面图形是( )
如图,这是一个由5个正方体组成的立体图形,从上面看得到的平面图形是( )



 已知,如图所示,折叠长方形OABC的一边BC,使点B落在AO边的点D处,如果AB=8,BC=10.
已知,如图所示,折叠长方形OABC的一边BC,使点B落在AO边的点D处,如果AB=8,BC=10.