题目内容
15.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=116°时,则∠EPC=64°.

分析 (1)先利用正方形的性质得,BA=BC,∠ABD=∠CBD=45°,则根据“SAS”可判定△ABP≌△CBP,所以PA=PC,于是得到PC=PE;
(2)利用△ABP≌△CBP得到∠PAB=∠PCB,根据等角的余角相等得到∠PAD=∠PCD,再利用PA=PE得到∠PAE=∠E,所以∠PCD=∠E,然后利用三角形内角和定理得到∠CPF=∠EDF=90°,
(3)根据菱形的性质得到BA=BC,∠ABD=∠CBD=58°,∠ADC=∠ABC=116°,则∠EDC=64°,与(2)同样的方法证明∠CPF=∠EDF=64°.
解答 (1)证明:∵四边形ABCD为正方形,
∴BA=BC,∠ABD=∠CBD=45°,
在△ABP和△CBP中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△CBP,
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)解:∵△ABP≌△CBP,
∴∠PAB=∠PCB,
∴∠PAD=∠PCD,
∵PA=PE,
∴∠PAE=∠E,
∴∠PCD=∠E,
而∠DFE=∠PFC,
∴∠CPF=∠EDF=90°,
(3)∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD=58°,∠ADC=∠ABC=116°,
∴∠EDC=64°,
在△ABP和△CBP中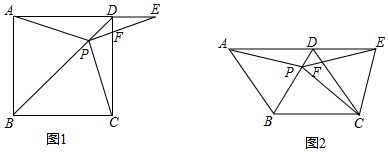
$\left\{\begin{array}{l}{BA=BC}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△CBP,
∴PA=PC,∠PAB=∠PCB,
∴∠PAD=∠PCP,
∵PA=PE,
∴∠PAD=∠PEA,
∴∠PCD=∠PED
而∠DFE=∠PFC,
∴∠CPF=∠EDF=64°.
故答案为64°.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.

(Ⅰ)根据题意,填写下表:
| 购买种子的数量/kg | 1.5 | 2 | 3.5 | 4 | … |
| 付款金额/元 | 7.5 | 10 | 16 | 8 | … |
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
 如图,已知OA⊥OC,∠BOC=2∠AOB,则∠AOB的度数等于30°.
如图,已知OA⊥OC,∠BOC=2∠AOB,则∠AOB的度数等于30°. 已知平行四边形ABCD的对角线相交于点O,且AC=12,BD=8,BC=5,则△AOD的周长=15.
已知平行四边形ABCD的对角线相交于点O,且AC=12,BD=8,BC=5,则△AOD的周长=15.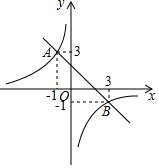 如图所示,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,则关于x的不等式kx+b<$\frac{m}{x}$的解集为-1<x<0或x>3.
如图所示,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,则关于x的不等式kx+b<$\frac{m}{x}$的解集为-1<x<0或x>3. 如图,在平行四边形ABCD中,BC=8cm,AB=6cm,BE平分∠ABC交AD边于点E,则线段DE的长度为2cm.
如图,在平行四边形ABCD中,BC=8cm,AB=6cm,BE平分∠ABC交AD边于点E,则线段DE的长度为2cm.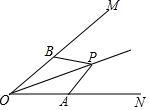 如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).