题目内容
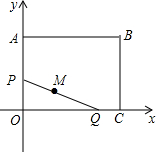 如图,矩形OABC的顶点B的坐标为B(8,7),动点P从原点O出发,以每秒2个单位的速度沿折线OA-AB运动,到点B时停止,同时,动点Q从点C出发,以每秒1个单位的速度在线段CO上运动,当一个点停止时,另一个点也随之而停止.在运动过程中,当线段PQ恰好经过点M(3,2)时,运动时间t的值是________.
如图,矩形OABC的顶点B的坐标为B(8,7),动点P从原点O出发,以每秒2个单位的速度沿折线OA-AB运动,到点B时停止,同时,动点Q从点C出发,以每秒1个单位的速度在线段CO上运动,当一个点停止时,另一个点也随之而停止.在运动过程中,当线段PQ恰好经过点M(3,2)时,运动时间t的值是________.
2或5
分析:设直线PQ的方程为y=kx+b(k≠0).分类讨论:当点P在线段OA上和点P在线段AB上运动时两种情况.把点P、Q、M的坐标分别代入函数解析式,通过方程组来求t的值.
解答: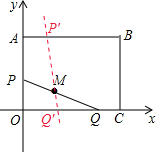 解:设直线PQ的方程为y=kx+b(k≠0).
解:设直线PQ的方程为y=kx+b(k≠0).
∵矩形OABC的顶点B的坐标为B(8,7),
∴OA=7,OC=8.
①当点P在线段OA上,即0≤t<3.5时,如图,P(0,2t)、Q(8-t,0).
∵直线PQ经过点M(3,2),
∴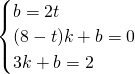 .
.
解得t=2;
②当点P在线段AB上,即3.5≤t<7时,如图,P′(15-2t,7)、Q(8-t,0).
∵直线PQ经过点M(3,2),
∴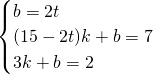 .
.
解得,t=5;
综上所述,t的值是2或5.
故答案是:2或5.
点评:本题考查了一次函数综合题.注意,对于动点问题需要分类讨论,以防错解或漏解.
分析:设直线PQ的方程为y=kx+b(k≠0).分类讨论:当点P在线段OA上和点P在线段AB上运动时两种情况.把点P、Q、M的坐标分别代入函数解析式,通过方程组来求t的值.
解答:
 解:设直线PQ的方程为y=kx+b(k≠0).
解:设直线PQ的方程为y=kx+b(k≠0).∵矩形OABC的顶点B的坐标为B(8,7),
∴OA=7,OC=8.
①当点P在线段OA上,即0≤t<3.5时,如图,P(0,2t)、Q(8-t,0).
∵直线PQ经过点M(3,2),
∴
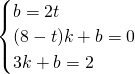 .
.解得t=2;
②当点P在线段AB上,即3.5≤t<7时,如图,P′(15-2t,7)、Q(8-t,0).
∵直线PQ经过点M(3,2),
∴
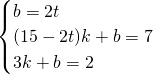 .
.解得,t=5;
综上所述,t的值是2或5.
故答案是:2或5.
点评:本题考查了一次函数综合题.注意,对于动点问题需要分类讨论,以防错解或漏解.

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是