题目内容
2.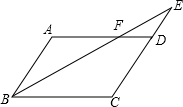 如图,在平行四边形ABCD中,E为CD延长线上的一点,BE交AD于F,DE=$\frac{1}{2}$CD=$\frac{1}{2}$AB
如图,在平行四边形ABCD中,E为CD延长线上的一点,BE交AD于F,DE=$\frac{1}{2}$CD=$\frac{1}{2}$AB(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求?ABCD的面积.
分析 (1)只要证明∠A=∠C,∠ABF=∠E即可解决问题;
(2)利用相似三角形的性质,分别求出△ABF,△EBC的面积即可解决问题;
解答 (1)证明:∵四边形ABCD是平行四边形
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB .
.
(2)∵DE∥AB,
∴△EDF∽△BAF,
∵$\frac{DE}{AB}$=$\frac{DE}{CD}$=$\frac{1}{2}$,S△DEF=2
∴S△ABF=8
∵DF∥BC,
∴△EDF∽△ECB,
∵ED:EC=1:3,
∴S△EBC=18
∴S平行四边形ABCD=8+18-2=24.
点评 本题考查平行四边形的性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.中国很早就开始使用负数,中国古代数学著作《九章算术》的“方程”一章在世界数学史首次正式引入负数,如果收入200元,记作:+200元,那么-60元表示( )
| A. | 支出140元 | B. | 收入140元 | C. | 支出60元 | D. | 收入60元 |
11.如果一元二次方程x2-ax+3=0经配方后,得(x-2)2=1,则a的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
5.在第49届世界乒乓球锦标赛中,男子单打决赛在我国选手马琳和王励勤之间展开,双方苦战七局,最终王励勤以4:3获得胜利,七局比分如下表:
(1)请将七局比分的相关数据的分析结果,直接填入下表中(结果精确到0.1).
(2)中央电视台在此次现场直播时,开展了“短信互动,有奖况猜”活动,凡是参与短信互动且预测结果正确的观众,都能参加“乒乓大礼包”的投资活动,据不完全统计,约有32000名观众参与了此次短信互动活动,其中有50%的观众预测王励勤获胜.陈明同学参加了本次“短信互动”活动,并预测了王励勤获胜,如果从中抽取80名幸运观众,赠送“乒乓大礼包”一份,那么陈明同学中奖的概率有多大?
| 局数 姓名 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 马 琳 | 11 | 11 | 5 | 11 | 8 | 9 | 6 |
| 王励勤 | 9 | 7 | 11 | 8 | 11 | 11 | 11 |
| 分析结果 姓名 | 平均分 | 众数 | 中位数 |
| 马 琳 | 8.7 | 11 | 9.0 |
| 王励勤 | 9.7 | 11 | 11 |
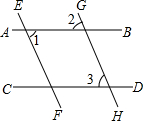 完成下面推理过程
完成下面推理过程 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)