题目内容
14．已知m、n是关于x的一元二次方程x2-2ax+a2+a-2=0的两实根，那么m+n的最大值是4．分析 先根据判别式的意义确定a≤2，再根据根与系数的关系得到m+n=2a，然后利用a的取值范围确定m+n的最大值．
解答 解：根据题意得△=4a2-4（a2+a-2）≥0，解得a≤2，
因为m+n=2a，
所以m+n≤4，
所以m+n的最大值为4．
故答案为4．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程根的判别式．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
4．下列事件是随机事件的是（ ）
| A． | 购买一张福利彩票中奖 | |
| B． | 400人中至少有两人的生日在同一天 | |
| C． | 有一名运动员奔跑的速度是30米/秒 | |
| D． | 在一个仅装着白球和黑球的袋中摸球，摸出红球 |
5．若二次函数y1=a1x2-1与二次函数y2=a2x2+3图象的形状完全相同，则a1与a2的关系为（ ）
| A． | a1=a2 | B． | a1=-a2 | C． | a1=±a2 | D． | 无法判断 |
2．若⊙O的半径为4，圆心O到直线l的距离为5，则直线l与⊙O的位置关系是（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 无法确定 |
9．
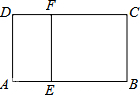如图，矩形ABCD∽矩形ADFE，AE=1，AB=4，则AD=（ ）
如图，矩形ABCD∽矩形ADFE，AE=1，AB=4，则AD=（ ）| A． | 2 | B． | 2.4 | C． | 2.5 | D． | 3 |
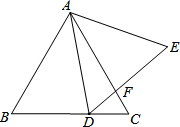如图，已知：△ABC和△ADE均为等边三角形，点D在BC边上，DE与AC交于点F
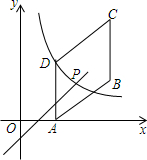如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3），反比例函数y=$\frac{m}{x}$（x＞0）的图象过点D，点P是一次函数y=kx+3-3k（k≠0）的图象与该反比例函数的一个公共点．对于一次函数y=kx+3-3k（k≠0），当y随x的增大而增大时，则点P横坐标a的取值范围$\frac{2}{3}$＜a＜3．
3．某商场一天中售出李宁运动鞋11双，其中各种尺码的鞋的销售量如下表所示，
那么这11双鞋的尺码组成的一组数据中，众数与中位数分别为（ ）
| 鞋的尺码（单位：cm） | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量（单位：双） | 1 | 2 | 2 | 5 | 1 |
| A． | 25，24.5 | B． | 24.5，25 | C． | 26，25 | D． | 25，25 |
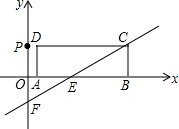已知长方形ABCD的边长AB=9，AD=3，现将此长方形置于平面直角坐标系中，使AB在x轴的正半轴上，经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E，与y轴交于点F．