题目内容
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若AB=13,sinB=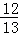 ,求CE的长.
,求CE的长.
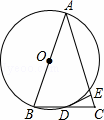
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°
∴AD⊥BC,又D是BC的中点,
∴AB=AC;
(2)证明:连接OD,
∵O、D分别是AB、BC的中点,
∴OD∥AC,
∴∠ODE=∠DEC=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)解:∵AB=13,sinB=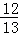 ,
,
∴ =
=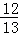 ,
,
∴AD=12,
∴由勾股定理得BD=5,
∴CD=5,
∵∠B=∠C,
∴ =
=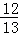 ,
,
∴DE= ,
,
∴根据勾股定理得CE= .
.


练习册系列答案
相关题目
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )

|
| A. | 点F | B. | 点E | C. | 点A | D. | 点C |
 0°.
0°.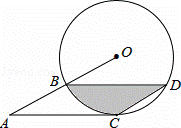
 的图象相交于A(4,2)、B(﹣2,m)两点,则一次函数的表达式为
的图象相交于A(4,2)、B(﹣2,m)两点,则一次函数的表达式为 

 C. 3
C. 3