Question

（1）若a、b为实数，且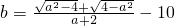，求a+b的立方根．
（2）我们在学习“实数”时，画了这样一个图，即以数轴上的单位长为“1”的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交数轴于点A，请根据图形回答下列问题：
①线段OA的长度是______．
②这种研究和解决问题的方式，体现了______的数学思想方法．
（将下列符合的选项序号填在横线上）
A．数形结合　 B．归纳　　C．换元　　D．消元．

Answer 1

解：（1）∵a²-4≥0，4-a²≥0，
∴a²-4=0，
又a+2≠0，
∴a=2；
b=-10，
∴a+b=-8，
故a+b的立方根为：-2．
（2）①∵OB²=1²+1²=2，
∴OB=，
∴OA=OB=；
②A．?
故答案为：①；②A．
分析：（1）由题意得a²-4≥0，4-a²≥0，故a²-4=0，又a+2≠0，可求出a的值，继而得出b的值，将a和b的值代入a+b，再根据立方根的概念求解即可；
（2）①首先根据勾股定理求出线段OB的长度，然后结合数轴的知识即可求解；
②根据所学的数学思想方法并结合题意即可求解．
点评：本题主要考查了勾股定理及实数与数轴之间的定义关系，此题综合性较强，不仅要结合图形，还需要熟悉平方根的定义．也要求学生了解数形结合的数学思想．