题目内容
若a、b为实数,且满足(a-1)2+
=0,则
+
+
+…+
=( )
| b-2 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2008)(b+2008) |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由于a、b为实数,且满足(a-1)2+
=0,所以a-1=0,b-2=0,所有可求得a=1,b=2,所求代数式变形为
+
+
+…+
=1-
+
-
+
+…+
-
,化简求值即可.
| b-2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2009×2010 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
解答:解:∵a、b为实数,满足(a-1)2+
=0,
又无论a,b为何值,(a-1)2≥0,
≥0,
∴a-1=0,b-2=0,
∴a=1,b=2,
∴
+
+
+…+
=
+
+
+…+
=1-
+
-
+
+…+
-
=
.
故选D.
| b-2 |
又无论a,b为何值,(a-1)2≥0,
| b-2 |
∴a-1=0,b-2=0,
∴a=1,b=2,
∴
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2008)(b+2008) |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2009×2010 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
=
| 2009 |
| 2010 |
故选D.
点评:本题考查了求代数式的值,对于代数式求值的题目,根据所给的已知条件,对所给代数式适当变形是解题的关键,变形的目标是能够利用已知条件,此类题目题型多,解题没有统一的规律可循.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 E点,直线NE与直线AB的交点G是否总满足PB•PG<10
E点,直线NE与直线AB的交点G是否总满足PB•PG<10 ,写出探索过程.
,写出探索过程.
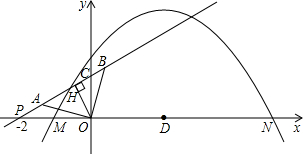
 点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG<
点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG< ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高. ,写出探索过程.
,写出探索过程.
 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高. ,写出探索过程.
,写出探索过程.