题目内容
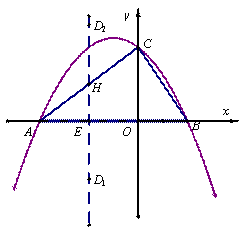
如图,抛物线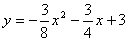 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上一动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l解析式。
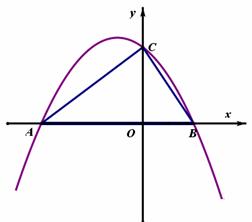
解:(1)令y=0,则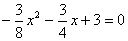 ,解得
,解得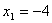 ,
,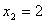
 ∴A(-4,0),B(2,0)
∴A(-4,0),B(2,0)
(2)∵抛物线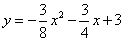 的对称轴为x=-1,与y轴交点C的坐标为(0,3)
的对称轴为x=-1,与y轴交点C的坐标为(0,3)
∴直线AC的解析式为 ,且当x=-1时,有
,且当x=-1时,有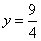
∴直线AC与对称轴x=-1的交点坐标为(-1,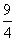 )
)
∵AB=6,CO=3
∴△ACB的面积为: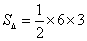 =9
=9
不妨设点D的坐标为(-1,a),当点D位于AC上方时,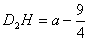 ,
,
∴△ACD的面积为: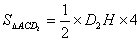 =9;解方程得:
=9;解方程得: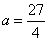
当点D位于AC下方时,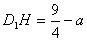 ,
,
∴△ACD的面积为: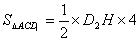 =9;解方程得:
=9;解方程得: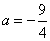 -
-
∴点D的坐标为 或
或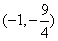
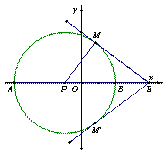
(3)如下图,以AB为直径作⊙P,当且仅当直线l与⊙P相切时符合题意,
∵Rt△PME中,∠PME=90°,PM=3,PE=5,
∴由勾股定理可得: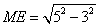 =4;利用三角形相似可以求得点M的坐标
=4;利用三角形相似可以求得点M的坐标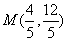
设直线l的解析式为: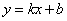 ,代入
,代入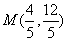 、E(4,0)可得方程组
、E(4,0)可得方程组
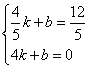 ;解方程组得:
;解方程组得: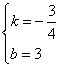
∴直线l的解析式为: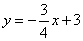
同理可得:直线l的另一个解析式为:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
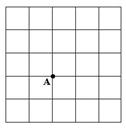
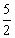 的格点等腰直角三角形.
的格点等腰直角三角形.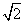 :
: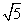 ,且最长边为5的格点三角形.
,且最长边为5的格点三角形.
 ,其中x=
,其中x= -1.
-1.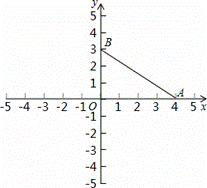
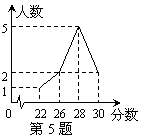


 肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )
肺,每年能为人类提供大约28.3亿吨的有机物.对于这个近似数,下列说法正确的是( )