题目内容
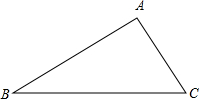 在△ABC中,BC=8,AC=4,点P是BC上一点,(P不与B、C重合)
在△ABC中,BC=8,AC=4,点P是BC上一点,(P不与B、C重合)(1)当点P距离点C多长时,△PAC与△ABC相似?请画出图形,说明理由.
(2)已知△ABC的面积为s,当△PAC与△ABC相似时,试求出△PAC的面积.
考点:相似三角形的判定
专题:
分析:(1)当PC=2时,△PAC∽△ABC,根据两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似证明即可;
(2)根据相似三角形的性质:面积比等于相似比的平方计算即可.
(2)根据相似三角形的性质:面积比等于相似比的平方计算即可.
解答:解:(1)如图所示:PC=2时,△PAC∽△ABC,
理由如下:
∵
=
,
=
,
∴
=
,
∴∠C=∠C,
∴△PAC∽△ABC;
(2)∵△PAC∽△ABC,
∴
=(
)2=
,
∴S△PAC=
s.

理由如下:
∵
| PC |
| AC |
| 1 |
| 2 |
| AC |
| BC |
| 1 |
| 2 |
∴
| PC |
| AC |
| AC |
| BC |
∴∠C=∠C,
∴△PAC∽△ABC;
(2)∵△PAC∽△ABC,
∴
| S△PAC |
| S△ABC |
| PC |
| AC |
| 1 |
| 4 |
∴S△PAC=
| 1 |
| 4 |
点评:本题考查了相似三角形的判定和性质,解题的关键是熟记相似三角形的各种判定方法以及各种性质.

练习册系列答案
相关题目
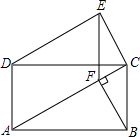 如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°,过点B作BF⊥AC于点F,连结EF,求证:
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°,过点B作BF⊥AC于点F,连结EF,求证: