题目内容
对于有理数x,用[x]表示不大于x的最大整数,请解方程 .
.
解:因为方程左边的第1、3项都是整数,
所以3y是整数.
注意到 ,
,
代入方程,得到 ,
,
 .
.
所以 是整数,3y是10的倍数.
是整数,3y是10的倍数.
令3y=10k,k是整数,
代入得 ,
,
其中,对于有理数x,x=x-[x].
所以有 ,
, .
.
当k取不同整数时, 的情况如下表:
的情况如下表:
k的可能值是-1和3,相应的 和y=10.
和y=10.
代入验算得到 或y=10.
或y=10.
故答案: 或y=10.
或y=10.
分析:由[x]表示不大于x的最大整数,得出[ ]整数,且
]整数,且 ,进而得到
,进而得到 是整数,得到关于k的不等式,并列举出所有可能,得到列表的结果,总结出符合要求的答案.
是整数,得到关于k的不等式,并列举出所有可能,得到列表的结果,总结出符合要求的答案.
点评:此题主要考查了取整函数的性质以及换元法解一元二次方程,假设3y=10k,k是整数,得出 的取值范围是解决问题的关键.
的取值范围是解决问题的关键.
所以3y是整数.
注意到
 ,
,代入方程,得到
 ,
, .
.所以
 是整数,3y是10的倍数.
是整数,3y是10的倍数.令3y=10k,k是整数,
代入得
 ,
,其中,对于有理数x,x=x-[x].
所以有
 ,
, .
.当k取不同整数时,
 的情况如下表:
的情况如下表:| k | ≤-2 | =-1 | =0 | =1 | =2 | =3 | >3 |
1-k- | <-1 | =- | =1 | =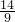 | = | =0 | <-1 |
 和y=10.
和y=10.代入验算得到
 或y=10.
或y=10.故答案:
 或y=10.
或y=10.分析:由[x]表示不大于x的最大整数,得出[
 ]整数,且
]整数,且 ,进而得到
,进而得到 是整数,得到关于k的不等式,并列举出所有可能,得到列表的结果,总结出符合要求的答案.
是整数,得到关于k的不等式,并列举出所有可能,得到列表的结果,总结出符合要求的答案.点评:此题主要考查了取整函数的性质以及换元法解一元二次方程,假设3y=10k,k是整数,得出
 的取值范围是解决问题的关键.
的取值范围是解决问题的关键. 
练习册系列答案
相关题目