题目内容
3. 如图,点C在线段AB上,点E、F分别是AC、BC的中点.
如图,点C在线段AB上,点E、F分别是AC、BC的中点.(1)若AC=8,BC=6,求线段EF的长;
(2)若AC+BC=a,你能求出EF的长度吗?并说明理由;
(3)若点C在AB的延长线上,且AC-BC=b,你能求出EF的长度吗?请画出图形,写出你的结论,并说明理由.
分析 (1)根据线段中点的性质,可得CE、CF的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得CE、CF的长,根据线段的和差,可得答案;
(3)根据线段中点的性质,可得CE、CF的长,根据线段的和差,可得答案.
解答 解:(1)∵点E,F分别是AC,BC的中点,AC=8,CB=6,
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4,CN=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∴EF=CE+CF=4+3=7;
(2)∵点E,F分别是AC,BC的中点,
∴CE=$\frac{1}{2}$AC,CF=$\frac{1}{2}$BC,
∴EF=CE+CF=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC )=$\frac{1}{2}$AB=$\frac{1}{2}$a;
(3)如图,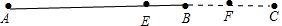
能求出EF的长,结论:EF=$\frac{1}{2}$b,
理由:∵点E,F分别是AC,BC的中点,AC=AB+BC,
∴CE=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC),CN=$\frac{1}{2}$BC,
∴EF=CE-CF=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC )=$\frac{1}{2}$b.
点评 本题考查了两点间的距离,利用了线段中点的性质得出CM、CN的长,线段的和差得出答案.

练习册系列答案
相关题目
13.哈西和谐大道跨线桥总投资250000000元,将250000000用科学记数法表示为( )
| A. | 25×107 | B. | 2.5×107 | C. | 2.5×108 | D. | 25×108 |
14.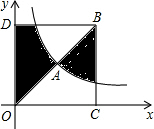 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上的一点,且点A的横坐标为2,连接OA并延长到点B,使AB=OA,过点B作x轴和y轴的垂线,垂足分别为C,D,则图中阴影部分的面积为( )| A. | 23 | B. | 18 | C. | 11 | D. | 8 |
15.分解因式2x3-18x结果正确的是( )
| A. | 2x(x+3)2 | B. | 2x(x-3)2 | C. | 2x(x2-9) | D. | 2x(x+3)(x-3) |
 如图,△ACB≌△DCE,∠ACD=50°,则∠BCE的度数为50°.
如图,△ACB≌△DCE,∠ACD=50°,则∠BCE的度数为50°.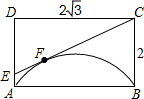 如图,矩形ABCD中,AB=2$\sqrt{3}$,AD=2,以AB为弦在矩形内部画一条120°的弧,过点C作直线CE,与$\widehat{AB}$切于点F,与AD边交于点E,那么DE的长是-18+8$\sqrt{6}$.
如图,矩形ABCD中,AB=2$\sqrt{3}$,AD=2,以AB为弦在矩形内部画一条120°的弧,过点C作直线CE,与$\widehat{AB}$切于点F,与AD边交于点E,那么DE的长是-18+8$\sqrt{6}$.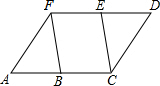 已知AC∥FD,AF∥CD,FB∥EC,求证:△AFB≌△DCE.
已知AC∥FD,AF∥CD,FB∥EC,求证:△AFB≌△DCE.