题目内容
| |||||||
答案:
解析:
解析:
|
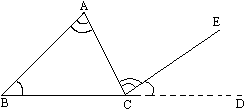
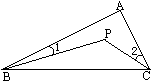
(1)∠ACD=∠A+∠B; (2)证明:①延长BP交AC于点D,由(1)得:∠BPC=∠2+∠PDC;∠PDC=∠A+∠1;∴∠BPC=∠2+∠A+∠1;②∵P是△ABC内一点∴∠1+∠2>0 ∴∠BPC-∠A=∠1+∠2>0 ∴∠BPC>∠A |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 =1-
=1-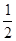
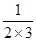 =
=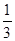
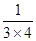 =
=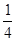 ……
…… 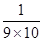 =
=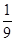 -
-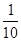
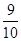
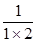 +
+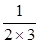 +…+
+…+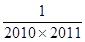 =
②
=
②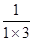 +
+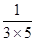 +
+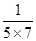 +…+
+…+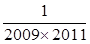 = 。
= 。