题目内容
【题目】阅读理解:
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是![]() ,
,![]() .
.
![]() 对于坐标平面内的一点P,给出如下定义:如果
对于坐标平面内的一点P,给出如下定义:如果![]() ,则称点P为线段AB的“等角点”
,则称点P为线段AB的“等角点”![]() 显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
![]() 设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和
设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和![]() 的半径;
的半径;
![]() 轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
![]() 当点P在y轴正半轴上运动时,
当点P在y轴正半轴上运动时,![]() 是否有最大值?如果有,说明此时
是否有最大值?如果有,说明此时![]() 最大的理由,并求出点P的坐标;如果没有请说明理由.
最大的理由,并求出点P的坐标;如果没有请说明理由.
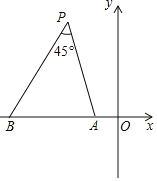
【答案】(1)①![]() 或
或![]() ,半径为
,半径为![]() ,②
,②![]() ,
,![]() .(2)
.(2)![]()
【解析】分析:
(1)①如下图1,连接BC、AC,则由“圆周角定理”可知∠ACB=2∠APB=90°,过点C作CH⊥AB于点H,则由已知条件根据“垂径定理”可得AH=BH=CH=3,从而可得OH=OA+AH=4,由此即可得到点C的坐标为(-4,3)或(-4,-3);此时在Rt△ACH中由勾股定理可求得![]() 的半径为
的半径为![]() ;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<
;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<![]() 可知,此时
可知,此时![]() C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
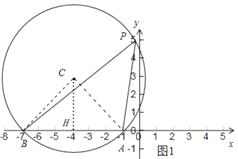
(2)如下图3,当过A,B的圆与y轴相切于点P时,∠![]() 最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点
最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,连接MA,MB,PA,PB,设MB交
,连接MA,MB,PA,PB,设MB交![]() E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=
E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=![]() ,从而可得OP=
,从而可得OP=![]() ,由此即可得到此时点P的坐标为
,由此即可得到此时点P的坐标为![]() .
.
详解:
(1)①如图1,
在x轴的上方,作以AB为斜边的直角三角形ACB,易知点A,B,P在![]() 上,连接
上,连接![]() 轴于点H,
轴于点H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由垂径定理可得,![]() ,
,
∴![]() ,
,![]() ,
,
所以![]() ,半径为
,半径为![]() ,
,
由对称性可知,点![]() 也满足条件.
也满足条件.
②![]() 轴的正半轴上存在线段AB的“等角点”.
轴的正半轴上存在线段AB的“等角点”.
如图2所示,

当圆心为![]() 时,过点C作
时,过点C作![]() 轴于点D,则
轴于点D,则![]() ,
,![]() ,
,
∵![]() 的半径为
的半径为![]() ,
,
∴![]() 与y轴相交,
与y轴相交,
设交点为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,CA,则
,CA,则![]() ,
,
∵![]() 轴,
轴,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
![]() 当过A,B的圆与y轴相切于点P时,
当过A,B的圆与y轴相切于点P时,![]() 最大.
最大.
理由如下:如果点P在y轴的正半轴上,如图3,
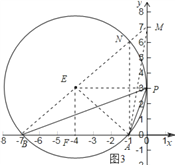
设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,
,
连接MA,MB,PA,PB,设MB交![]() 于点N,连接NA,
于点N,连接NA,
∵点P、点N在![]() 上,
上,
∴![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,即
,即![]() ,
,
此时,过点E作![]() 轴于点F,连接EA,EP,则
轴于点F,连接EA,EP,则![]() ,
,![]() ,
,
∵![]() 与y轴相切于点P,则
与y轴相切于点P,则![]() 轴,
轴,
∴四边形OPEF是矩形,![]() ,
,![]() ,
,
∴![]() 的半径为4,即
的半径为4,即![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()

 阅读快车系列答案
阅读快车系列答案