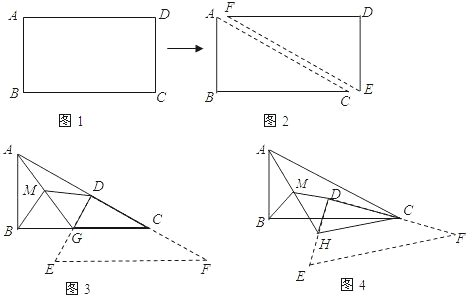
题目内容
如图1和图2,在△ABC中,AB=13,BC=14,cos∠ABC=![]() .
.
探究
在如图1,AH⊥BC于点H,则AH=________,AC=________,△ABC的面积S△ABC=________.
拓展
如图2,点D在AC上(可与点A,B重合),分别过点A,C作直线BD的垂线,垂足为E,F.设BD=x,AE=m,CF=n.(当点D与点A重合时,我们认为S△ABC=0.
(1)用含x,m或n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值.
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现
请你确定一条直线,使得A,B,C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
答案:
解析:
解析:
|
解:探究:12,15,84;3分 拓展:(1)由三角形面积公式,得 (2)由(1)得 由于 当 (3) 发现: 最小值为 |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目