题目内容
如图，已知线段AB=a，点C在直线AB上，AC=3AB．（1）用尺规作图画出点C；
（2）若点P在线段BC上，且BP：PC=2：3，D为线段PC的中点，求BD的长（用含a的代数式表示）；
（3）在（2）的条件下，若AD=3cm，求a的值．
考点：两点间的距离,列代数式
专题：计算题
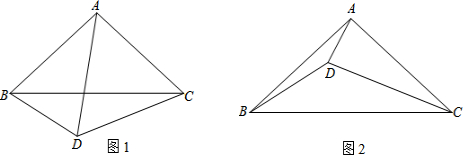
分析：（1）分两种情况画图：点C在线段AB的延长线上或C点在线段AB的反向延长线上；
（2）对于图1，BC=2a，由BP：PC=2：3可计算出BP=
BC=
a，PC=
BC=
a，再由D为线段PC的中点得到PD=
PC=
a，然后利用BD=BP+PD计算得BD=
a；
对于图2，BC=4a，由BP：PC=2：3可计算得BP=
BC=
a，PC=
BC=
a，再由D为线段PC的中点得到PD=
PC=
a，然后利用BD=BP+PD计算可得BD=
a；
（3）对于图1，先得到CD=PD=
a，再计算出AD=AC-CD=
a，则
a=3，然后解方程即可；
对于图2，先得到CD=PD=
a，利用计算出AD=BC-CD=
a，则
a=3，然后解方程即可．
（2）对于图1，BC=2a，由BP：PC=2：3可计算出BP=
| 2 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 7 |
| 5 |
对于图2，BC=4a，由BP：PC=2：3可计算得BP=
| 2 |
| 5 |
| 8 |
| 5 |
| 3 |
| 5 |
| 12 |
| 5 |
| 1 |
| 2 |
| 6 |
| 5 |
| 14 |
| 5 |
（3）对于图1，先得到CD=PD=
| 3 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
对于图2，先得到CD=PD=
| 14 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
解答：解：（1）如图所示：
当点C在线段AB的延长线上，如图1；
当C点在线段AB的反向延长线上时，如图2；
；
（2）对于图1，
∵AB=a，
∴AC=3a，
∴BC=2a，
∵BP：PC=2：3，
∴BP=
BC=
•2a=
a，PC=
BC=
a，
∵D为线段PC的中点，
∴PD=
PC=
a，
∴BD=BP+PD=
a+
a=
a；
对于图2，
BC=AB+AC=4a，
∵BP：PC=2：3，
∴BP=
BC=
•4a=
a，PC=
BC=
a，
∵D为线段PC的中点，
∴PD=
PC=
a，
∴BD=BP+PD=
a+
a=
a；
（3）对于图1，CD=PD=
a，AD=AC-CD=3a-
a=
a=3，解得a=
（cm）；
对于图2，CD=PD=
a，AD=BC-CD=4a-
a=
a=3，解得a=
（cm）．
当点C在线段AB的延长线上，如图1；
当C点在线段AB的反向延长线上时，如图2；
；（2）对于图1，
∵AB=a，
∴AC=3a，
∴BC=2a，
∵BP：PC=2：3，
∴BP=
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
∵D为线段PC的中点，
∴PD=
| 1 |
| 2 |
| 3 |
| 5 |
∴BD=BP+PD=
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 5 |
对于图2，
BC=AB+AC=4a，
∵BP：PC=2：3，
∴BP=
| 2 |
| 5 |
| 2 |
| 5 |
| 8 |
| 5 |
| 3 |
| 5 |
| 12 |
| 5 |
∵D为线段PC的中点，
∴PD=
| 1 |
| 2 |
| 6 |
| 5 |
∴BD=BP+PD=
| 8 |
| 5 |
| 6 |
| 5 |
| 14 |
| 5 |
（3）对于图1，CD=PD=
| 3 |
| 5 |
| 3 |
| 5 |
| 12 |
| 5 |
| 5 |
| 4 |
对于图2，CD=PD=
| 14 |
| 5 |
| 14 |
| 5 |
| 6 |
| 5 |
| 5 |
| 2 |
点评：本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．也考查了列代数式和分类讨论的思想．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、3a+2b=5ab |
| B、a3+a3=2a3 |
| C、4m3-m3=3 |
| D、4x2y-2xy2=2xy |
下列说法正确的是（ ）
| A、x的系数为0 | ||
B、-
| ||
| C、-5是一次单项式 | ||
D、
|
如图所示，点M，N在线段AB上，且MB=5cm，NB=14cm，N是线段AM的中点，则线段AB为