题目内容
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB. 如果点P
在直线y=x-1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.
(1)判断点C( ,
, ) 是否是线段AB的“邻近点”,并说明理由;
) 是否是线段AB的“邻近点”,并说明理由;
(2)若点Q (m,n)是线段AB的“邻近点”,求m的取值范围.
在直线y=x-1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“邻近点”.
(1)判断点C(
 ,
, ) 是否是线段AB的“邻近点”,并说明理由;
) 是否是线段AB的“邻近点”,并说明理由;(2)若点Q (m,n)是线段AB的“邻近点”,求m的取值范围.

(1)是,理由见解析(2)3<m<5
解:(1)点C( ,
, ) 是线段AB的“邻近点”。理由如下:
) 是线段AB的“邻近点”。理由如下:
∵ -1=
-1= ,∴点C(
,∴点C( ,
, )在直线y=x-1上.。
)在直线y=x-1上.。
∵点A的纵坐标与点B的纵坐标相同,∴ AB∥x轴。
∴C( ,
, ) 到线段AB的距离是3-
) 到线段AB的距离是3- =
= 。
。
∵ <1,∴C(
<1,∴C( ,
, )是线段AB的“邻近点”。
)是线段AB的“邻近点”。
(2)∵点Q(m,n)是线段AB的“邻近点”,∴点Q(m,n)在直线y=x-1上。
∴ n=m-1。
① 当m≥4时, n=m-1≥3。
又AB∥x轴,∴此时点Q(m,n)到线段AB的距离是n-3。
∴0≤n-3<1。∴4≤m<5。
② 当m<4时, n=m-1<3。
又AB∥x轴,∴ 此时点Q(m,n)到线段AB的距离是3-n。
∴0≤3-n<1。∴3<m<4。
综上所述, 3<m<5。
(1)验证点C( ,
, )满足“邻近点”的条件即可。
)满足“邻近点”的条件即可。
(2)分m≥4和m<4讨论即可
 ,
, ) 是线段AB的“邻近点”。理由如下:
) 是线段AB的“邻近点”。理由如下:∵
 -1=
-1= ,∴点C(
,∴点C( ,
, )在直线y=x-1上.。
)在直线y=x-1上.。∵点A的纵坐标与点B的纵坐标相同,∴ AB∥x轴。
∴C(
 ,
, ) 到线段AB的距离是3-
) 到线段AB的距离是3- =
= 。
。∵
 <1,∴C(
<1,∴C( ,
, )是线段AB的“邻近点”。
)是线段AB的“邻近点”。(2)∵点Q(m,n)是线段AB的“邻近点”,∴点Q(m,n)在直线y=x-1上。
∴ n=m-1。
① 当m≥4时, n=m-1≥3。
又AB∥x轴,∴此时点Q(m,n)到线段AB的距离是n-3。
∴0≤n-3<1。∴4≤m<5。
② 当m<4时, n=m-1<3。
又AB∥x轴,∴ 此时点Q(m,n)到线段AB的距离是3-n。
∴0≤3-n<1。∴3<m<4。
综上所述, 3<m<5。
(1)验证点C(
 ,
, )满足“邻近点”的条件即可。
)满足“邻近点”的条件即可。(2)分m≥4和m<4讨论即可

练习册系列答案
相关题目

 .
. 为何值时,一次函数的值大于反比例函数的值?
为何值时,一次函数的值大于反比例函数的值?
 轴上,顶点B的坐标为(4,6).若直线
轴上,顶点B的坐标为(4,6).若直线 将□ABCO分割成面积相等的两部分,则k的值是( )
将□ABCO分割成面积相等的两部分,则k的值是( )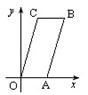


 的图象如右图所示,则结论:
的图象如右图所示,则结论: 的坐标为
的坐标为 ; ②当
; ②当 时,
时, ;
;  时,
时, ; ④当
; ④当 逐渐增大时,
逐渐增大时, 随着
随着 随着
随着