题目内容
12、在△ABC和△ADC中,有下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个正确的因果关系,则条件是
①AB=AD;②∠BAC=∠DAC或①AB=AD;③BC=DC
,结论为③BC=DC或②∠BAC=∠DAC
.分析:根据全等三角形的判定方法SAS,可知当①②为条件且AC为公共边时结论③成立;根据全等三角形的判定方法SSS,可知当①③为条件且AC为公共边时结论②立;
解答:解:方案一∵AB=AD,∠BAC=∠DAC,AC为公共边,
∴△ABC≌△ADC,
∴BC=DC;
方案二:∵AB=AD,BC=DC,AC为公共边,
∴△ABC≌△ADC,
∴∠BAC=∠DAC.
故答案为:条件:①AB=AD;②∠BAC=∠DAC或①AB=AD;③BC=DC;结论为:③BC=DC或∠BAC=∠DAC.
∴△ABC≌△ADC,
∴BC=DC;
方案二:∵AB=AD,BC=DC,AC为公共边,
∴△ABC≌△ADC,
∴∠BAC=∠DAC.
故答案为:条件:①AB=AD;②∠BAC=∠DAC或①AB=AD;③BC=DC;结论为:③BC=DC或∠BAC=∠DAC.
点评:本题考查了全等三角形的判定及性质,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 3、如图,在△ABC和△ADC中,AB=AD,要判定△ABC≌△ADC,还需要增加的条件是
3、如图,在△ABC和△ADC中,AB=AD,要判定△ABC≌△ADC,还需要增加的条件是
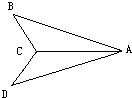 20、在△ABC和△ADC中,给出下列三个论断:①BC=DC;②∠BAC=∠DAC;③AB=AD.
20、在△ABC和△ADC中,给出下列三个论断:①BC=DC;②∠BAC=∠DAC;③AB=AD.