题目内容
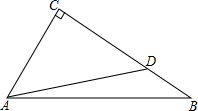 如图,在△ABC中,∠C=90°,cosB=
如图,在△ABC中,∠C=90°,cosB=| 4 |
| 5 |
(1)求BD的长;
(2)求cot∠BAD的值.
考点:解直角三角形
专题:
分析:(1)根据余弦值可求得BC,由勾股定理可求得AC,则可求得BD的长;
(2)过D作DE⊥AB于E,在Rt△BDE中可求得DE和BE,可求得AE,在Rt△ADE中可求得cot∠BAD.
(2)过D作DE⊥AB于E,在Rt△BDE中可求得DE和BE,可求得AE,在Rt△ADE中可求得cot∠BAD.
解答:解:(1)∵∠C=90°,cosB=
,
∴
=
,即
=
,
解得BC=8,
在Rt△ABC中,AB=10,BC=8,由勾股定理可求得AC=6,
∴CD=AC=6,
∴BD=BC-CD=8-6=2;
(2)如图,过D作DE⊥AB于E,
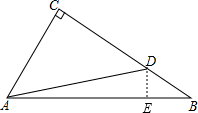
在Rt△BED中,BD=2,cosB=
,
∴
=
,即
=
,
解得BE=
,
则AE=10-
=
,
在Rt△BDE中,BD=2,BE=
,由勾股定理可求得DE=
,
在Rt△ADE中,cot∠BAD=
=
=7.
| 4 |
| 5 |
∴
| BC |
| AB |
| 4 |
| 5 |
| BC |
| 10 |
| 4 |
| 5 |
解得BC=8,
在Rt△ABC中,AB=10,BC=8,由勾股定理可求得AC=6,
∴CD=AC=6,
∴BD=BC-CD=8-6=2;
(2)如图,过D作DE⊥AB于E,

在Rt△BED中,BD=2,cosB=
| 4 |
| 5 |
∴
| BE |
| BD |
| 4 |
| 5 |
| BE |
| 2 |
| 4 |
| 5 |
解得BE=
| 8 |
| 5 |
则AE=10-
| 8 |
| 5 |
| 42 |
| 5 |
在Rt△BDE中,BD=2,BE=
| 8 |
| 5 |
| 6 |
| 5 |
在Rt△ADE中,cot∠BAD=
| AE |
| DE |
| ||
|
点评:本题主要考查三角函数的定义,掌握在直角三角形中正弦=
、余弦=
、正切=
,余切=
是解题的关键.
| 对边 |
| 斜边 |
| 邻边 |
| 斜边 |
| 对边 |
| 邻边 |
| 邻边 |
| 对边 |

练习册系列答案
相关题目
一个多边形的内角和与外角和相加之后的结果是2520°,则这个多边形的边数为( )
| A、12 | B、13 | C、14 | D、15 |
下列各式成立的是( )
| A、-2<(-0.6)2<(-1)3 |
| B、-2<(-1)3<(-0.6)2 |
| C、(-0.6)2<(-1)3<-2 |
| D、(-1)3<-2<(-0.6)2 |
-(-3)的绝对值是( )
| A、-3 | B、+3 | C、0 | D、4 |
下列计算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
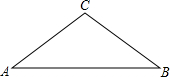 如图,△ABC中,BC=5,AC=5,AB=8.
如图,△ABC中,BC=5,AC=5,AB=8. 如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,
如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,