题目内容
 如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交
如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交 于点C,则图中阴影部分的面积为________.
于点C,则图中阴影部分的面积为________.

分析:根据已知条件得出△AOC是等边三角形,进而利用:S扇形BOC-小弓形面积=S扇形AOC-小弓形面积=S△AOC求出即可.
解答:
 解:连接AC,CO,过点O作OD⊥AC于点D,
解:连接AC,CO,过点O作OD⊥AC于点D,∵在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交
 于点C,
于点C,∴AC=AO=CO=2,
∴△AOC是等边三角形,
∴∠AOC=∠BOC=60°,
∵OD⊥AC,
∴DO=AOsin60°=
 ,
,∴S△AOC=
 ×AC×DO=
×AC×DO= ,
,∵图中阴影部分的面积为:S扇形BOC-小弓形面积=S扇形AOC-小弓形面积=S△AOC=
 .
.故答案为:
 .
.点评:此题主要考查了扇形的有关计算以及等边三角形判定和面积求法等知识,根据已知得出:S扇形BOC-小弓形面积=S扇形AOC-小弓形面积=S△AOC是解题关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
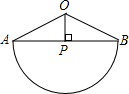 如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.
如图,在扇形OAB中,OP⊥AB于点P,半径为4,OP=2.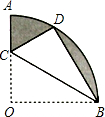 (2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在
(2012•吉林)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在
 如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在
如图,在扇形OAB中,∠AOB=110°,半径OA=12,将扇形OAB沿过点B的直线折叠,点O恰好落在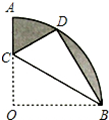 (2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落
(2013•平顶山二模)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将沿过点B的直线折叠,点O恰好落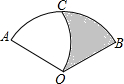 (2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交
(2013•老河口市模拟)如图,在扇形OAB中,∠AOB=120°,OA=2,以A为圆心,AO长为半径画弧交