题目内容
18. 如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=3,AC=3$\sqrt{2}$.判断△ACD的形状,并证明你的结论.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=3,AC=3$\sqrt{2}$.判断△ACD的形状,并证明你的结论.
分析 首先利用已知条件和勾股定理可证明BC=AB,进而可得∠BCA=∠BAC=45°,再根据已知条件可得∠CAD=135-45°=90°,所以三角形CAD是直角三角形.
解答 证明:Rt△ABC中,∠ABC=90°,
AB=1,AC=$\sqrt{2}$,
∴BC2=($\sqrt{2}$)2-12=1,
∴BC=AB,
∴∠BCA=∠BAC=45°,
又∵∠BAD=135°,
∴∠CAD=135-45°=90°,
∴△ACD是直角三角形.
点评 本题考查了勾股定理的运用,等腰直角三角形,熟练掌握等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
6. 如图,O是△ABC的∠ABC,∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=16,则△ODE的周长是( )
如图,O是△ABC的∠ABC,∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=16,则△ODE的周长是( )
 如图,O是△ABC的∠ABC,∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=16,则△ODE的周长是( )
如图,O是△ABC的∠ABC,∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=16,则△ODE的周长是( )| A. | 16 | B. | 10 | C. | 8 | D. | 以上都不对 |
13.某地夏天的最低气温是13℃,最高气温是30℃,则这天气温是t(℃)的取值范围是( )
| A. | t<13 | B. | t>30 | C. | 13<t<30 | D. | 13≤t≤30 |
8.为了弘扬传统文化,某校举办了一次国学知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上为合格,达到9分以上(包括9分)为优秀,这次竞赛中,甲、乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
(2)小明对同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是甲(填“甲”或“乙”)组的学生;
(3)甲组同学说他们的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩更好于甲组.请你给出三条支持乙组同学观点的理由.

(1)补充完成下面的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.7 | 6 | 3.4 | 90% | 20% |
| 乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(3)甲组同学说他们的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩更好于甲组.请你给出三条支持乙组同学观点的理由.
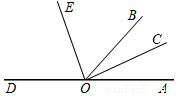 如图,已知点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=20°,求∠BOE的度数.
如图,已知点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=20°,求∠BOE的度数.


