题目内容
 如图所示,在△ABC中,AD平分∠BAC,FE⊥AD于点E,交BC的延长线于点F,连接AF,恰有∠FAC=∠B.求证:EF是AD的垂直平分线.
如图所示,在△ABC中,AD平分∠BAC,FE⊥AD于点E,交BC的延长线于点F,连接AF,恰有∠FAC=∠B.求证:EF是AD的垂直平分线.考点:线段垂直平分线的性质
专题:证明题
分析:因为FE⊥AD于点E,所以再证明AE=DE即可得到EF是AD的垂直平分线,若要证明AE=DE,可通过证明△FAE≌△FDE得到.
解答:证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠FAC=∠B,
∴∠EDF=∠EAF,
∵FE⊥AD于点E,
∴∠AEF=∠DEF=90°,
在△FAE和△FDE中
,
∴△FAE≌△FDE,
∴AE=DE,
∴EF是AD的垂直平分线.
∴∠BAD=∠CAD,
∵∠FAC=∠B,
∴∠EDF=∠EAF,
∵FE⊥AD于点E,
∴∠AEF=∠DEF=90°,
在△FAE和△FDE中
|
∴△FAE≌△FDE,
∴AE=DE,
∴EF是AD的垂直平分线.
点评:此题考查了全等三角形的判定和性质、垂直平分线的性质、三角形外角的性质以及角平分线的定义.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将二次根式
进行分母有理化的结果是( )
| ||
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
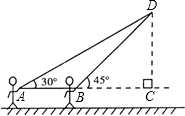 放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号)
放风筝是广受喜爱的一种运动,星期天的上午小明在大运河广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树捎上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了B处,此时风筝BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°,点B距大树CD的水平距离为8米.请你求出小明此时所收回的风筝线的长度是多少米?(结果保留根号) 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.