题目内容
已知二次函数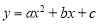 (
(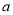 为常数,且
为常数,且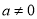 )的图象过点A(0,1),B(1,-2)和点C(-1,6).
)的图象过点A(0,1),B(1,-2)和点C(-1,6).
(1)求二次函数表达式;
(2)若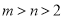 ,比较
,比较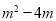 与
与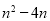 的大小;
的大小;
(3)将抛物线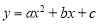 平移,平移后图象的顶点为
平移,平移后图象的顶点为 ,若平移后的抛物线与直线
,若平移后的抛物线与直线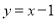 有且只有一个公共点,请用含
有且只有一个公共点,请用含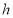 的代数式表示
的代数式表示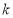 .
.
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)把A、B、C的坐标代入二次函数,即可求得结论;
(2)利用开口向上时,在对称轴右边,二次函数的值随x增大而增大可得结论;
(3)由(1)知, .设平移后的抛物线的表达式为
.设平移后的抛物线的表达式为 ,由直线与抛物线有且只有一个公共点,得方程
,由直线与抛物线有且只有一个公共点,得方程 有两个相等的实数根,整理即可得出h,k的关系式.
有两个相等的实数根,整理即可得出h,k的关系式.
试题解析:(1)∵抛物线过点 ,
, ,
, ,∴
,∴ ,∴
,∴ ,∴
,∴ ;
;
(2)∵当 时,
时, 随
随 的增大而增大,∴当
的增大而增大,∴当 时,
时, ,即
,即 ;
;
(3) 由(1)知, .设平移后的抛物线的表达式为
.设平移后的抛物线的表达式为 ,∵直线与抛物线有且只有一个公共点,∴方程
,∵直线与抛物线有且只有一个公共点,∴方程 有两个相等的实数根,整理得:
有两个相等的实数根,整理得: ,∴
,∴ ,∴
,∴ .
.
考点:二次函数综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,OC=3,那么⊙O的半径等于 .
,OC=3,那么⊙O的半径等于 .
 ,CE=1.求
,CE=1.求 的长度.
的长度.
 在第一象限的图象上有两点
在第一象限的图象上有两点 ,
, ,它们的横坐标分别是2,6,则△
,它们的横坐标分别是2,6,则△ 的面积是 .
的面积是 .
 与y轴交于(0,3)点.
与y轴交于(0,3)点. 的根是多少?
的根是多少? ?
?
 B.
B. C.
C. D.
D.