题目内容
 我们定义:在等腰三角形中,腰与底边的比叫做等腰三角形的正度.已知△ABC中,AB=AC,D是底边上的一个动点(D与B、C不重合).
我们定义:在等腰三角形中,腰与底边的比叫做等腰三角形的正度.已知△ABC中,AB=AC,D是底边上的一个动点(D与B、C不重合).(1)张强同学认为一定存在点D,使△ABD具有正度,你认为张强同学的说法正确吗?如果正确,请加以证明;不正确,举一个反例说明;
(2)如图,∠A>∠ABC,△ABC的正度为
| 5 |
| 8 |
考点:解直角三角形,等腰三角形的性质
专题:
分析:(1)不一定存在点D,使△ABD具有正度,反例:当∠BAC<∠ABC,只需说明△ABD不可能为等腰三角形即可.
(2)由△ABC的正度为
,周长为18,求出△ABC的三条边的长,然后分两种情况讨论:①当AB=BD=5时,如图(2),求出AD即可;②当AD=BD时,如图(3),求出AD即可.
(2)由△ABC的正度为
| 5 |
| 8 |
解答:解:(1)不一定存在点D,使△ABD具有正度,
反例:当∠BAC<∠ABC时,如图(1)
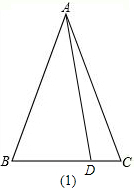
∵AB=AC,
∴∠B=∠C,
∵∠BAC<∠ABC,
∴∠BAD<∠ABC,
∵∠ADB是△ADC的外角,
∴∠ADB>∠C,
∴∠ADB>∠ABC>∠BAD,
∴AB>AD>BD,
∴△ABD不可能为等腰三角形,
∴不一定存在点D,使△ABD具有正度.
(2)存在.
∵△ABC的正度为
,
∴
=
,
设:AB=5x,BC=8x,则AC=5x,
∵△ABC的周长为18,
∴AB+BC+AC=18,
即:18x=18,
∴x=1,
∴AB=5x=5,BC=8x=8,AC=5x=5,
分两种情况:
①当AB=BD=5时,如图(2)
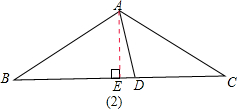
过点A作AE⊥BC于点E,
∵AB=AC,
∴BE=CE=
BC=4,
∵BD=5,
∴DE=BD-BE=1,
在Rt△ABE中,
由勾股定理得:AE=3,
在Rt△AED中,
由勾股定理得:AD=
,
∴△ABD的正度=
=
=
;
②当AD=BD时,如图(3)
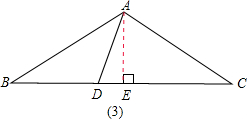
由①可知:BE=4,AE=3,
∵AD=BD,
∴DE=BE-BD=4-AD,
在Rt△ADE中,由勾股定理得:
AD2-DE2=AE2,
即:AD2-(4-AD)2=32,
解得:AD=
,
∴△ABD的正度=
=
=
.
综上所述存在两个点D,使△ABD具有正度.△ABD的正度为
或
.
反例:当∠BAC<∠ABC时,如图(1)

∵AB=AC,
∴∠B=∠C,
∵∠BAC<∠ABC,
∴∠BAD<∠ABC,
∵∠ADB是△ADC的外角,
∴∠ADB>∠C,
∴∠ADB>∠ABC>∠BAD,
∴AB>AD>BD,
∴△ABD不可能为等腰三角形,
∴不一定存在点D,使△ABD具有正度.
(2)存在.
∵△ABC的正度为
| 5 |
| 8 |
∴
| AB |
| BC |
| 5 |
| 8 |
设:AB=5x,BC=8x,则AC=5x,
∵△ABC的周长为18,
∴AB+BC+AC=18,
即:18x=18,
∴x=1,
∴AB=5x=5,BC=8x=8,AC=5x=5,
分两种情况:
①当AB=BD=5时,如图(2)

过点A作AE⊥BC于点E,
∵AB=AC,
∴BE=CE=
| 1 |
| 2 |
∵BD=5,
∴DE=BD-BE=1,
在Rt△ABE中,
由勾股定理得:AE=3,
在Rt△AED中,
由勾股定理得:AD=
| 10 |
∴△ABD的正度=
| AB |
| AD |
| 5 | ||
|
| ||
| 2 |
②当AD=BD时,如图(3)

由①可知:BE=4,AE=3,
∵AD=BD,
∴DE=BE-BD=4-AD,
在Rt△ADE中,由勾股定理得:
AD2-DE2=AE2,
即:AD2-(4-AD)2=32,
解得:AD=
| 25 |
| 8 |
∴△ABD的正度=
| AD |
| AB |
| ||
| 5 |
| 5 |
| 8 |
综上所述存在两个点D,使△ABD具有正度.△ABD的正度为
| ||
| 2 |
| 5 |
| 8 |
点评:此题考查了等腰三角形的性质,解题的关键是:理解正度的含义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点,求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.
已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点,求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等. 如图,在一个草地的中央有一个边长为10m的正方形鱼塘,池边A、B、C、D处各有一棵大树,且AB=BC=CD=3m,现用4m长的绳子将一头牛拴在其中一棵树上,问将牛拴在哪棵树上,可使牛的活动范围最大?
如图,在一个草地的中央有一个边长为10m的正方形鱼塘,池边A、B、C、D处各有一棵大树,且AB=BC=CD=3m,现用4m长的绳子将一头牛拴在其中一棵树上,问将牛拴在哪棵树上,可使牛的活动范围最大? 如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD;则∠CEB的度数
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD;则∠CEB的度数