题目内容
16.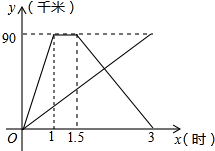 如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.
如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若乙出发后2小时和甲相遇.求乙从A地到B地用了多长时间?
(3)相遇前,何时甲、乙两人的距离最大?最大距离是多少?
分析 (1)首先设y与x之间的函数关系式为y=kx+b,根据图象可得直线经过(1.5,90)(3,0),利用待定系数法把此两点坐标代入y=kx+b,即可求出一次函数关系式;
(2)利用甲从B地返回A地的过程中,y与x之间的函数关系式算出y的值,即可得到2小时时骑摩托车所行驶的路程,再根据路程与时间算出摩托车的速度,再用总路程90千米÷摩托车的速度可得乙从A地到B地用了多长时间;
(3)根据图示得到当x=1时,他们的距离最大.利用待定系数法求得乙的距离与时间关系式,把x=1代入即可求得乙距A地的距离,然后求差即可.
解答 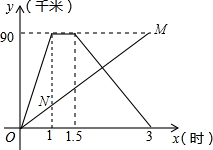 解:(1)设甲从B地返回A地的过程中,y与x之间的函数关系式为y=kx+b(k≠0),根据题意得:
解:(1)设甲从B地返回A地的过程中,y与x之间的函数关系式为y=kx+b(k≠0),根据题意得:
$\left\{\begin{array}{l}{3k+b=0}\\{1.5k+b=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-60}\\{b=180}\end{array}\right.$.
故y=-60x+180(1.5≤x≤3);
(2)当x=2时,y=-60×2+180=60.
∴骑摩托车的速度为60÷2=30(千米/时),
∴乙从A地到B地用时为90÷30=3(小时);
(3)由图示知,由(2)知,M(3,90),
所以直线OM的解析式为:y=30x.
如图所示,当x=1时,甲、乙两人的距离最大.
当x=1时,y=30,即N(1,30),所以此时的距离:90-30=60(千米).
答:相遇前,出发1小时时甲、乙两人的距离最大,最大距离是60千米.
点评 此题主要考查了一次函数的应用,关键是看懂图象所表示的意义,利用待定系数法求出甲从B地返回A地的过程中,y与x之间的函数关系式.

练习册系列答案
相关题目
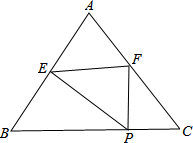 如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.
如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.