Question

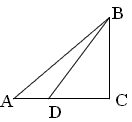
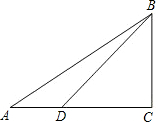已知，如图∠A=37°，∠C=90°，∠ADB=135°，AB=5、求△ABC的周长及AD的长，（精确到0.1）
参考数据：sin37°=0.602    cos37°=0.899    tan37°=0.75．

Answer 1

分析：在直角△ABC中，即可根据三角函数解得BC与AC，即可求得△ABC的面积；
已知ADB=135°，即可求得∠BDC的度数，在直角△BCD中依据三角函数即可求得CD，AC与CD的差即为AD的长．

解答：解：∵∠C=90°
∴sinA=

BC

AB

cosA=

AC

AB

（1分）
∴sin37°=

BC

5

cos37°=

AC

5

∴BC=0.602×5=3.010AC=0.899×5=4.495（3分）
∴△ABC的周长=AB+BC+AC=5+3.010+4.495=12.505≈12.5（4分）
∵∠ADC=135°
∴∠BDC=45°
∵∠C=90°
∴DC=BC=3.010（5分）
∴AD=AC-DC=4.495-3.010=1.485≈1.5（6分）

点评：本题主要考查了解直角三角形的方法，已知一个角的一个三角函数值即可求得其它的三角函数值，并且在一个直角三角形中，已知一边和一个锐角就能求出其它的边和角．