题目内容
如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（ ）
A．AE=OE
B．∠AOC=60°
C．CE=DE
D．OE=
CE
【答案】分析：根据垂径定理：垂直于弦的直径垂直于弦，得到E为CD的中点，可得出CE=DE，故选项C一定正确；而选项A、B、D不一定成立．
解答：解：A、由CD不一定垂直平分OA，即AE不一定等于OE，得到本选项不一定正确；
B、由∠AOC不一定为60°，得到本选项不一定正确；
C、∵⊙O的直径AB⊥弦CD，
∴CE=DE，本选项一定正确；
D、由OE不一定等于
CE，本选项不一定正确，
故选C
点评：此题考查了垂径定理，垂径定理的内容为：垂直于弦的直径平分于弦，且平分弦所对的弧，熟练掌握垂径定理是解本题的关键．
解答：解：A、由CD不一定垂直平分OA，即AE不一定等于OE，得到本选项不一定正确；
B、由∠AOC不一定为60°，得到本选项不一定正确；
C、∵⊙O的直径AB⊥弦CD，
∴CE=DE，本选项一定正确；
D、由OE不一定等于
CE，本选项不一定正确，故选C
点评：此题考查了垂径定理，垂径定理的内容为：垂直于弦的直径平分于弦，且平分弦所对的弧，熟练掌握垂径定理是解本题的关键．
练习册系列答案
相关题目
2、如图，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是（ ）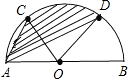
如图，已知半圆的直径AB=4cm，点C、D是这个半圆的三等分点，则弦AC、AD和
22、如图，已知⊙O的直径为10，P为⊙O内一点，且OP=4，则过点P且长度小于6的弦共有
如图，已知⊙O的直径AB与弦AC的夹角∠CAB=27°，过点C作⊙O的切线交AB延长线于点D，则∠ADC的度数为（ ）
（2010•邢台二模）如图，已知⊙O的直径AB与弦AC的夹角为31°，过C点的切线PC与AB的延长线交于点P，则∠P等于（ ）