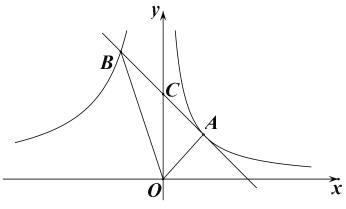
题目内容
【题目】如图,在平面直角坐标系中A为直线y=![]() x﹣1上一点,过原点O的直线与反比例函数y=﹣
x﹣1上一点,过原点O的直线与反比例函数y=﹣![]() 图象交于点B,C.若△ABC为等边三角形,则点A的坐标为_____.
图象交于点B,C.若△ABC为等边三角形,则点A的坐标为_____.
【答案】(﹣2![]() ,﹣
,﹣![]() )
)
【解析】
观察图象可知点A只能在第三象限,如图设△ABC是等边三角形,作BM⊥x轴于M,AN⊥x轴于N.设B(m,﹣![]() ),利用相似三角形的判定得到△OMB∽△ANO,进而求出点A的坐标(用m表示),再利用待定系数法求出m即可.
),利用相似三角形的判定得到△OMB∽△ANO,进而求出点A的坐标(用m表示),再利用待定系数法求出m即可.
解:观察图象可知点A只能在第三象限,如图设△ABC是等边三角形,作BM⊥x轴于M,AN⊥x轴于N,
设B(m,﹣![]() ),
),

由题意,B,C关于原点O对称,
∴OB=OC,
∵△ABC是等边三角形,
∴OA⊥BC,OA=![]() OB,
OB,
∴∠AOB=∠OMB=∠ONA=90°,
∴∠BOM+∠AON=90°,∠NAO+∠AON=90°,
∴∠BOM=∠NAO,
∴△OMB∽△ANO,
∴![]() ,
,
∵OM=﹣m,BM=﹣![]() ,
,
∴ON=﹣![]() ,AN=﹣
,AN=﹣![]() m,
m,
∴A(![]() ,
,![]() m),
m),
∵点A在直线y=![]() x﹣1上,
x﹣1上,
∴![]() m=
m=![]() ﹣1,
﹣1,
解得m=﹣![]() 或
或![]() (舍弃),
(舍弃),
∴A(﹣2![]() ,﹣
,﹣![]() ).
).
故答案为:(﹣2![]() ,﹣
,﹣![]() ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司计划投资![]() 万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为
万元引进一条汽车配件流水生产线,经过调研知道该流水生产线的年产量为![]() 件,每件总成本为
件,每件总成本为![]() 万元,每件出厂价
万元,每件出厂价![]() 万元;流水生产线投产后,从第
万元;流水生产线投产后,从第![]() 年到第
年到第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)如下表:
(万元)如下表:
第 |
|
|
|
|
|
| ··· |
维修、保养费用累计 |
|
|
|
|
|
| ··· |
若上表中第![]() 年的维修、保养费用累计
年的维修、保养费用累计![]() (万元)与
(万元)与![]() 的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
的数量关系符合我们已经学过的一次函数、二次函数、反比例函数中某一个.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)投产第几年该公司可收回![]() 万元的投资?
万元的投资?
(3)投产多少年后,该流水线要报废(规定当年的盈利不大于维修、保养费用累计即报费)?