题目内容
雅美服装厂现有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料0.6m,B种布料0.9m,可获利润45元;做一套N型号的时装需用A种布料1.1m,B种布料0.4m,可获利润50元.若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获得的总利润为y元.
(1)请帮雅美服装厂设计出生产方案;
(2)求y(元)与x(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
解:(1)设生产N型号的时装套数为x,则生产M型号的时装为(80﹣x),由题意,得
 ,
,
解得:40≤x≤44.
∵x为整数,
∴x取40,41,42,43,44.
∴有5种方案:
方案1:M型号40套,N型号40套;
方案2:M型号39套,N型号41套;
方案3:M型号38套,N型号42套;
方案4:M型号37套,N型号43套;
方案5:M型号36套,N型号44套;
(2)由题意,得
y=45(80﹣x)+50x=5x+3600.
∵k=5>0,
∴y随x的增大而增大,
∴当x=44时,y最大=3820元.
∴选择方案5所获利润最大.

练习册系列答案
相关题目
 ,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
 知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y
知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y =________.
=________.
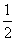 ︱+(
︱+(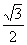 -cosB)2=0, 则∠C=___________________.
-cosB)2=0, 则∠C=___________________.