题目内容
19.(1)计算:(-$\sqrt{5}$)2+($\sqrt{2}$+1)($\sqrt{2}$-1)-$\sqrt{\frac{2}{3}}$×$\sqrt{1\frac{1}{2}}$(2)解方程:x2-2x-1=0.
分析 (1)根据二次根式的混合运算顺序,首先计算乘方和开方,然后计算乘法,最后从左向右依次计算,求出算式(-$\sqrt{5}$)2+($\sqrt{2}$+1)($\sqrt{2}$-1)-$\sqrt{\frac{2}{3}}$×$\sqrt{1\frac{1}{2}}$的值是多少即可.
(2)应用配方法,求出一元二次方程x2-2x-1=0的解是多少即可.
解答 解:(1)(-$\sqrt{5}$)2+($\sqrt{2}$+1)($\sqrt{2}$-1)-$\sqrt{\frac{2}{3}}$×$\sqrt{1\frac{1}{2}}$
=5+[${(\sqrt{2})}^{2}$-12]$-\frac{\sqrt{6}}{3}×\frac{\sqrt{6}}{2}$
=5+[2-1]-1
=5+1-1
=5
(2)∵x2-2x-1=0,
∴(x-1)2=2,
∴x-1=±$\sqrt{2}$,
解得x=1+$\sqrt{2}$,x=1-$\sqrt{2}$,
即x2-2x-1=0的解是x=1+$\sqrt{2}$,x=1-$\sqrt{2}$.
点评 (1)此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.
(2)此题还考查了配方法解一元二次方程问题,要熟练掌握,解答此题的关键是要明确用配方法解一元二次方程的步骤:①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案| A. | 1 | B. | 0 | C. | 3 | D. | -3 |
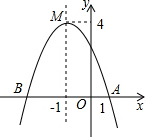 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )| A. | a<0 | B. | 当x=-1时,函数y有最小值4 | ||
| C. | 对称轴是直线=-1 | D. | 点B的坐标为(-3,0) |
| A. | 第三、四象限 | B. | 第一、二象限 | C. | 第二、三象限 | D. | 第一、二、三象限 |
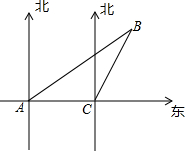 三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)
三个小岛A、B、C的位置如图所示,在A处测得小岛B在A的北偏东52°方向,在C处测得小岛B在C的北偏东26°方向,且A、B之间的距离是1000海里,求:小岛C在小岛A的正东方向多少海里?(精确到1海里)