题目内容
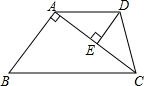 如图,梯形ABCD中,AD∥BC,∠BAC=90°,DE⊥AC于E点.
如图,梯形ABCD中,AD∥BC,∠BAC=90°,DE⊥AC于E点.
(1)△ABC与△EDA相似吗?说明理由.
(2)若AB=6,BC=10,AD=DC;
①求线段DE的长;
②求梯形ABCD的面积.
解:(1)△ABC与△EDA相似,
理由是:∵AD∥BC,
∴∠DAE=∠ACB,
∵∠BAC=90°,DE⊥AC,
∴∠AED=∠BAC=90°,
∴△ABC∽△EDA;
(2)①在Rt△BAC中,AB=6,BC=10,由勾股定理得:AC=8,
∵AD=DC,DE⊥AC,
∴AE=CE= AC=4,
AC=4,
∵△ABC∽△EDA,
∴ =
= ,
,
∴ =
=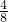 ,
,
∴DE=3;
②S梯形ABCD=S△ADC+S△BAC
= ×AC×DE+
×AC×DE+ ×AB×AC
×AB×AC
= ×8×3+
×8×3+ ×6×8
×6×8
=36.
分析:(1)求出∠DAE=∠ACB,∠AED=∠BAC=90°,根据相似三角形的判定推出即可;
(2)①求出AC,求出AE,根据相似三角形的性质得出比例式,代入求出即可;②分别求出△BAC和△ACD的面积,相加即可求出答案.
点评:本题考查了相似三角形的性质和判定,平行线性质,梯形的性质,三角形的面积,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力.
理由是:∵AD∥BC,
∴∠DAE=∠ACB,
∵∠BAC=90°,DE⊥AC,
∴∠AED=∠BAC=90°,
∴△ABC∽△EDA;
(2)①在Rt△BAC中,AB=6,BC=10,由勾股定理得:AC=8,
∵AD=DC,DE⊥AC,
∴AE=CE=
 AC=4,
AC=4,∵△ABC∽△EDA,
∴
 =
= ,
,∴
 =
=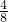 ,
,∴DE=3;
②S梯形ABCD=S△ADC+S△BAC
=
 ×AC×DE+
×AC×DE+ ×AB×AC
×AB×AC=
 ×8×3+
×8×3+ ×6×8
×6×8=36.
分析:(1)求出∠DAE=∠ACB,∠AED=∠BAC=90°,根据相似三角形的判定推出即可;
(2)①求出AC,求出AE,根据相似三角形的性质得出比例式,代入求出即可;②分别求出△BAC和△ACD的面积,相加即可求出答案.
点评:本题考查了相似三角形的性质和判定,平行线性质,梯形的性质,三角形的面积,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.