题目内容
2.某织布厂有150名工人,为了提高经济效益,增设制衣项目.已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.(1)一天中制衣所获利润P=100x(用含x的式子表示);
(2)一天中剩余布所获利润Q=(9000-72x)(用含x的式子表示);
(3)一天当中安排多少名工人制衣时,所获利润为11806元?
分析 (1)根据一天的利润=每件利润×件数×人数,列出代数式;
(2)安排x名工人制衣,则织布的人数为(150-x),根据利润=(人数×米数-制衣用去的布)×每米利润,列代数式即可;
(3)根据总利润=11806,列方程求解即可.
解答 解:(1)由题意得,P=25×4×x=100x.
故答案是:100x;
(2)由题意得,Q=[(150-x)×30-6x]×2=9000-72x.
故答案是:(9000-72x);
(3)由题意得,100x+9000-72x=11806,
解得:x≈100.21.
答:一天当中安排100名工人制衣时,所获利润为11806元.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
12.完成某项工作,甲独做需a小时,乙独做需b小时,则两人合作完成这项工作的80%,所需要的时间是( )
| A. | $\frac{4}{5}(a+b)$小时 | B. | $\frac{4}{5}(\frac{1}{a}+\frac{1}{b})$小时 | C. | $\frac{4ab}{5(a+b)}$小时 | D. | $\frac{ab}{a+b}$小时 |
10.室内温度10℃,室外温度是-3℃,那么室内温度比室外温度高( )
| A. | 13℃ | B. | 7℃ | C. | -7℃ | D. | -13℃ |
17.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
| A. | 4cm | B. | 5cm | C. | 7cm | D. | 14cm |
7.小明买了m千克苹果,花了n元,则每千克苹果是( )
| A. | $\frac{m}{n}$元 | B. | $\frac{n}{m}$元 | C. | mn元 | D. | (n-m)元 |
12.如图图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图案中白色正方形的个数为( )
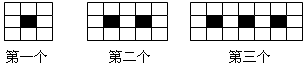

| A. | 50 | B. | 53 | C. | 55 | D. | 60 |