题目内容
7.已知方程组$\left\{\begin{array}{l}{ax+by=-3①}\\{2x+cy=7②}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$,某同学由于看错第②个方程中y的系数,接的方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,请你想一想,原来的方程组是怎样的吗?分析 把$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$代入方程组中两个方程得到关于a与b的方程,求出c的值,再将$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$代入方程组第一个方程得到关于a与b的方程,联立求出a与b的值,确定出方程组即可.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{a-b=-3①}\\{2-c=7②}\end{array}\right.$,
解得:c=-5,
把$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$代入①得:5a+b=-3,
联立得:$\left\{\begin{array}{l}{5a+b=-3}\\{a-b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
则原方程组为$\left\{\begin{array}{l}{-x+2y=-3}\\{2x-5y=7}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.我国是一个严重缺水的国家,淡水资源总量为28000亿立方米,人均淡水资源低于世界平均水平,因此,珍惜水、保护水是我们每一位公民的责任,其中数据28000用科学记数法表示为( )
| A. | 28×103 | B. | 2.8×104 | C. | 0.28×105 | D. | 2.8×105 |
2. 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
 图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )
图中的阴影旋转一个角度后,能互相重合,这个角度可以是( )| A. | 30° | B. | 45° | C. | 120° | D. | 90° |
12.轨道交通给人们的出行提供了便捷的服务,据悉,上海轨道交通19号线即将开建,一期规划为自川桥路站至长兴岛,设6站,全长约为20600米.二期、远期将延伸到崇明岛、横沙岛,届时崇明县三岛将全通地铁.将20600用科学记数法表示应为( )
| A. | 2.06×105 | B. | 20.6×103 | C. | 2.06×104 | D. | 0.206×105 |
19.某学校在开展“节约每一滴水”的活动中,从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是540吨.
| 节水量(单位:吨) | 1 | 1.2 | 1.5 | 2 | 2.5 |
| 同学数 | 4 | 5 | 6 | 3 | 2 |
16.5月19日为中国旅游日,宁波推出“读万卷书,行万里路,游宁波景”的主题系列旅游惠民活动,市民王先生准备在优惠日当天上午从奉化溪口、象山影视城、宁海浙东大峡谷中随机选择一个地点;下午从宁波动物园、伍山石窟、东钱湖风景区中随机选择一个地点游玩,则王先生恰好上午选中宁海浙东大峡谷,下午选中东钱湖风景区这两个地的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
17.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害.0.0000025用科学记数法可表示为( )
| A. | 2.5×10-5 | B. | 0.25×10-7 | C. | 2.5×10-6 | D. | 25×10-5 |
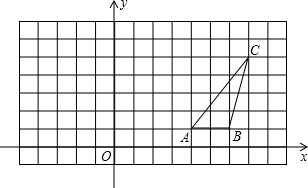 如图,△ABC的顶点坐标分别为A(4,1)、B(6,1)、C(7,5).
如图,△ABC的顶点坐标分别为A(4,1)、B(6,1)、C(7,5).