题目内容
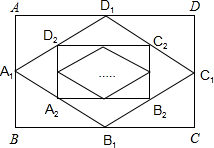 如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn=________.
如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn=________.
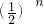
分析:首先探求四边形A1B1C1D1的面积和矩形ABCD的面积关系:连接BD,根据三角形的中位线定理,得A1D1∥BD,A1D1=
 BD,则△AA1D1∽△ABD,且面积比是
BD,则△AA1D1∽△ABD,且面积比是 ,进而得到四边形A1B1C1D1的面积为矩形ABCD的面积的一半,即
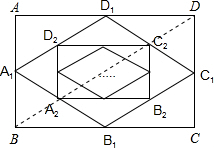
,进而得到四边形A1B1C1D1的面积为矩形ABCD的面积的一半,即 .推而广之,则Sn=
.推而广之,则Sn= .
.解答:
 解:连接BD.
解:连接BD.根据三角形的中位线定理,得
A1D1∥BD,A1D1=
 BD,
BD,∴△AA1D1∽△ABD,且面积比是
 .
.∴四边形A1B1C1D1的面积为矩形ABCD的面积的一半,即
 .
.推而广之,则Sn=
 .
.点评:此题主要是运用了三角形的中位线定理以及相似三角形的判定和性质.

练习册系列答案
相关题目
 如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,
如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm, m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).
m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6). 点A运动.
点A运动. (2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )
(2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( ) 如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<
如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<