Question

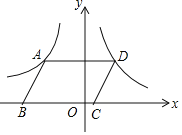
【题目】某厂家一种摩托车如图所示，它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°．

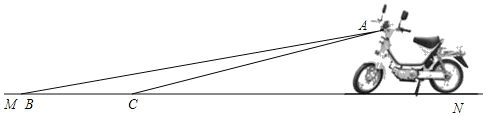
（1）该车大灯照亮地面的宽度BC是1.4m，求大灯A与地面距离约是多少？

（2）一般正常人从发现危险到做出刹车动作的反应时间是0.2s，从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离，某人以60km/h的速度驾驶该车，突然遇到危险情况，立即刹车直到摩托车停止，在这个过程刹车距离是m，请判断（1）中的该车大灯A的地面高度是否能满足最小安全距离的要去，若不能该如何调整A的高度？（参考数据：sin8°≈，tan8°≈，sin10°≈，tan10°≈）

Answer 1

【答案】（1）大灯A与地面距离约是1m；（2）该车大灯的设计不能满足最小安全距离的要求，应该调整到A的高度为1.28m．

【解析】

（1）过A作AD⊥MN于D，设AD＝xm，解直角三角形求出BD，CD，根据BC＝1.4m构建方程即可解问题．
（2）本题可先计算出最小安全距离是多少，然后与大灯能照到的最远距离进行比较，即可得出是否合格的结论；再利用三角函数求出满足最小安全距离时AD的值即可

（1）过A作AD⊥MN于点D，设AD＝xm，

由题意得：∠ACD＝10°，∠ABD＝8°，

在Rt△ACD中，tan∠ACD＝ ，

解得：CD＝5.6x（m），

在Rt△ABD中，tan∠ABD＝，

解得：BD＝7x（m），

∴BC＝7x﹣5.6x＝1.4（m），

∴x＝1，

答：大灯A与地面距离约是1m；

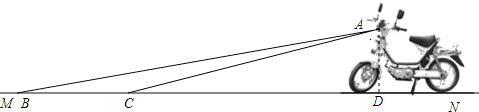
（2）该车大灯的设计不能满足最小安全距离的要求，

∵以60 km/h的速度驾驶，

∴速度可以化为：m/s，

则最小安全距离为：×0.2+＝8（m），

∵大灯能照到的最远距离是BD＝7m，

∴该车大灯的设计不能满足最小安全距离的要求，

当BD＝8m时，，即

∴AD＝1.28m，

∴应该调整到A的高度为1.28m．