题目内容
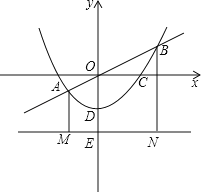
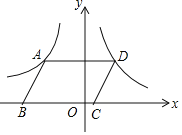
【题目】如图，在平面直角坐标系中，ABCD的顶点B，C在x轴上，A，D两点分别在反比例函数y＝﹣
（x＜0）与y＝
（x＞0）的图象上，若ABCD的面积为4，则k的值为：_____．
【答案】1
【解析】
连接OA、OD，如图，利用平行四边形的性质得AD垂直y轴，则利用反比例函数的比例系数k的几何意义得到S△OAE和S△ODE，所以S△OAD＝
+
，，然后根据平行四边形的面积公式可得到ABCD的面积＝2S△OAD＝4，即可求出k的值．
连接OA、OD，如图，
∵四边形ABCD为平行四边形，
∴AD垂直y轴，
∴S△OAE＝
×|﹣3|＝，S△ODE＝×|k|，
∴S△OAD＝+，
∵ABCD的面积＝2S△OAD＝4．
∴3+|k|＝4，
∵k＞0，
解得k＝1，
故答案为1．
练习册系列答案
阅读快车系列答案
相关题目
