题目内容
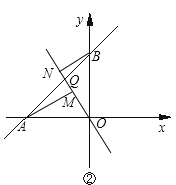
【题目】把一张长方形纸片![]() 按如图方式折叠,使顶点
按如图方式折叠,使顶点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() .若
.若![]() ,
,![]() ,
,
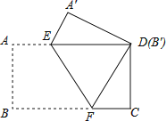
(1)求![]() 的长;
的长;
(2)求重叠部分的面积.
【答案】(1)5;(2)10.
【解析】
(1)根据折叠的性质知:BF=DF,设DF=x,用x表示出FC,在Rt△DCF中,利用勾股定理可求得DF的长;
(2)作FH⊥AD于点H,求得FH,由折叠的性质和平行线的性质证得∠EFD=∠DEF,得出DE=DF,进一步利用三角形的面积计算公式即可求解.
解:(1)设DF=x,由折叠可知BF=DF=x,
∴FC=BC-BF=8-x,
∵四边形ABCD为长方形,
∴DC=AB=4,∠C=90°,
在Rt△DCF中,DF2=DC2+FC2,
∴x2=42+(8-x)2,解得x=5,
∴DF=5;
(2)作FH⊥AD于点H,则FH=AB=4,
由折叠可知,∠EFB=∠EFD,
∵AD∥BC,∴∠DEF=∠EFB,∴∠EFD=∠DEF,
∴ED=DF=5,
∴S△DEF=![]() EDFH=
EDFH=![]() ×5×4=10.
×5×4=10.


练习册系列答案
相关题目
【题目】为响应我市创建“全国文明城市”的号召,我区某校举办了一次“秀美巴中,绿色家园”主题演讲比赛,满分![]() 分,得分均为整数,成绩大于等于
分,得分均为整数,成绩大于等于![]() 分为合格,大于等于
分为合格,大于等于![]() 分为优秀,这次演讲比赛中甲、乙两组学生(各
分为优秀,这次演讲比赛中甲、乙两组学生(各![]() 名学生)成绩分布的条形统计图如下图:
名学生)成绩分布的条形统计图如下图:

(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 |
|
|
|
|
| |
乙 |
|
|
|
|
|
(2)小王同学说:“这次演讲赛我得了![]() 分,在我们小组中排名属中游略偏上!”观察上表可知,小王是________组的学生;(填“甲”或“乙”)
分,在我们小组中排名属中游略偏上!”观察上表可知,小王是________组的学生;(填“甲”或“乙”)
(3)结合两个小组的成绩分析,你觉得哪个组的成绩更好一些?说说你的理由.