题目内容
已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;

(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
(1);(2) ;(3)E的坐标为(-2,-4)或(4,-4). 【解析】试题分析:(1)把A、B两点带入抛物线解析式,求得a、b的值,即可得到抛物线解析式; (2)由AC=AB且点C在点A的左侧,及线段CP是线段CA、CB的比例中项,可得CP=, 由两边对应成比例且夹角相等的三角形相似,可得△CPA∽△CBP,由此∠CPA= ∠CBP. 过P作PH⊥x轴于H,易得PH=4...
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
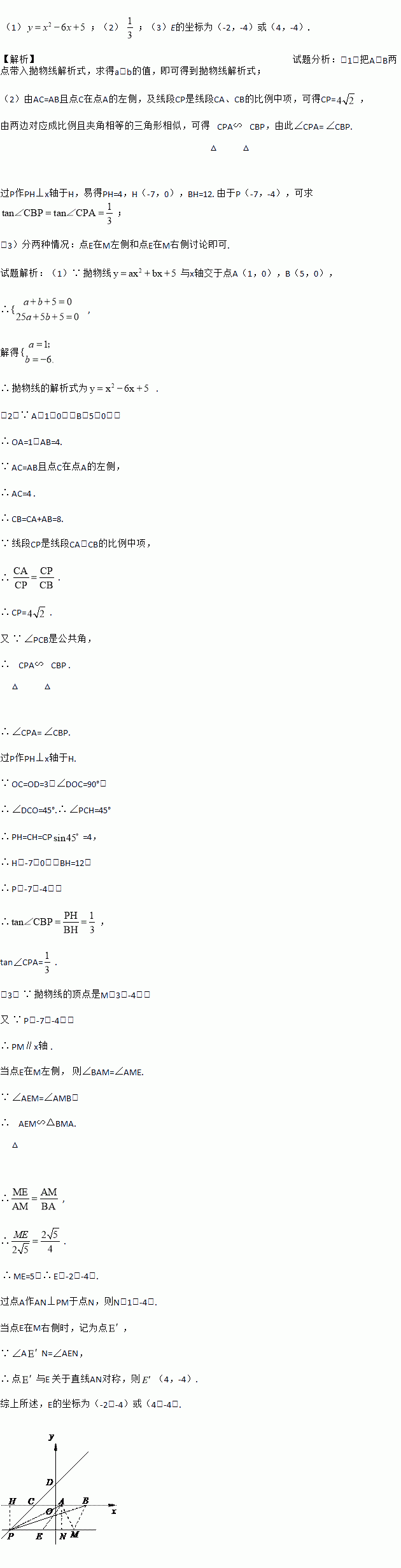


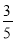 B.
B. 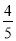 C.
C. 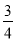 D.
D. 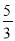
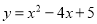 向左平移4个单位,求平移后抛物线的表达式、顶点坐标
向左平移4个单位,求平移后抛物线的表达式、顶点坐标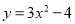 的最低点的坐标是 .
的最低点的坐标是 .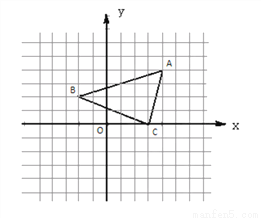

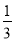 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.