题目内容
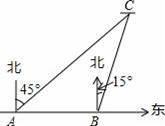
2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.飞机上有239名乘客,其中154名是中国同胞.中国政府启动了全面应急和搜救机制,派出多艘中国舰船在相关海域进行搜救.如图,某日在南印度洋海域有两艘自西向东航行的搜救船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两船同时测得在A的东北方向,B的北偏东15°方向有疑似物C,求此时疑似物C与搜救船A,B的距离各是多少(结果保留根号)

【考点】解直角三角形的应用-方向角问题.
【分析】首先过点B作BD⊥AC于D,由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,则可求得∠ACB的度数,然后利用三角函数的知识求解即可求得答案.
【解答】解:过点B作BD⊥AC于D.
由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=30°.
在Rt△ABD中,AD=BD=AB•sin∠BAD=20×
 =10
=10
 (海里),
(海里),
在Rt△BCD中,BC=
 =
=
 =20
=20
 (海里),
(海里),
DC=
 =
=
 =10
=10
 (海里),
(海里),
∴AD+CD=10
 +10
+10
 =10(
=10(
 +
+
 )(海里).
)(海里).
答:疑似物C与搜救船A的距离是10(
 +
+
 )海里,与搜救船B的距离是20
)海里,与搜救船B的距离是20
 海里.
海里.


【点评】此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
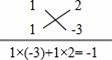


 +
+
 =2;
=2; 

 在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .
在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .