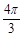题目内容
 如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为
如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为
- A.

- B.

- C.

- D.

A
分析:过点O作OD⊥AB,先根据等腰三角形的性质得出∠OAD的度数,由直角三角形的性质得出OD的长,再根据S阴影=S扇形OAB-S△AOB进行计算即可.
解答: 解:过点O作OD⊥AB,
解:过点O作OD⊥AB,
∵∠AOB=120°,OA=2,
∴∠OAD= =
= =30°,
=30°,
∴OD= OA=
OA= ×2=1,AD=
×2=1,AD= =
= =
= ,
,
∴AB=2AD=2 ,
,
∴S阴影=S扇形OAB-S△AOB= -
- ×2
×2 ×1=
×1=
 .
.
故选A.
点评:本题考查的是扇形面积的计算及三角形的面积,根据题意得出S阴影=S扇形OAB-S△AOB是解答此题的关键.
分析:过点O作OD⊥AB,先根据等腰三角形的性质得出∠OAD的度数,由直角三角形的性质得出OD的长,再根据S阴影=S扇形OAB-S△AOB进行计算即可.
解答:
 解:过点O作OD⊥AB,
解:过点O作OD⊥AB,∵∠AOB=120°,OA=2,
∴∠OAD=
 =
= =30°,
=30°,∴OD=
 OA=
OA= ×2=1,AD=
×2=1,AD= =
= =
= ,
,∴AB=2AD=2
 ,
,∴S阴影=S扇形OAB-S△AOB=
 -
- ×2
×2 ×1=
×1=
 .
.故选A.
点评:本题考查的是扇形面积的计算及三角形的面积,根据题意得出S阴影=S扇形OAB-S△AOB是解答此题的关键.

练习册系列答案
相关题目
如图所示,扇形AOB的中心角为60°,半径为6,C、D分别是
的三等分点,则阴影部分的面积是( )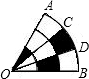
 |
| AB |

| A、16π | B、6π | C、2π | D、π |
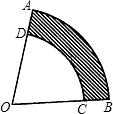 如图所示,扇形AOB中,∠AOB=60°,AD=3cm,
如图所示,扇形AOB中,∠AOB=60°,AD=3cm,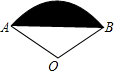 (2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( )
(2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( ) 如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为
如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为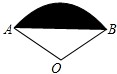
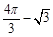 B.
B.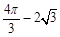 C.
C.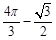 D.
D.