题目内容
9.解方程组:(1)$\left\{\begin{array}{l}{y=3x-9}\\{2x-y=5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2(2x+y)=7}\\{3y+4x=9-2y}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{y=3x-9①}\\{2x-y=5②}\end{array}\right.$,
把①代入②得:2x-3x+9=5,
解得:x=4,
把x=4代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{4x+2y=7①}\\{4x+5y=9②}\end{array}\right.$,
②-①得:3y=2,即y=$\frac{2}{3}$,
把y=$\frac{2}{3}$代入①得:x=$\frac{17}{12}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{17}{12}}\\{y=\frac{2}{3}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
20. 某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
 某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
某地有两所中学和两条相交叉的公路(点M,N表示中学,AO,BO表示公路).计划修建一个饭馆:希望饭馆到两所中学的距离相等,到两条公路的距离也相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)
4.将等积式ac=bd改写成比例式,其中正确的是( )
| A. | $\frac{a}{b}=\frac{c}{d}$ | B. | $\frac{a}{b}=\frac{d}{c}$ | C. | $\frac{a}{c}=\frac{b}{d}$ | D. | $\frac{a}{d}=\frac{c}{b}$ |
18.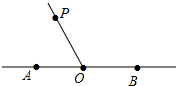 如图,下列语句中,描述错误的是( )
如图,下列语句中,描述错误的是( )
 如图,下列语句中,描述错误的是( )
如图,下列语句中,描述错误的是( )| A. | 点O在直线AB上 | B. | 直线AB与射线OP相交于点O | ||
| C. | 点P在直线AB上 | D. | ∠AOP与∠BOP互为补角 |
 如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )



 某服装公司试销一种成本为每件50元的T恤衫,试销中得出销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
某服装公司试销一种成本为每件50元的T恤衫,试销中得出销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).