题目内容
18．
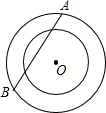如图所示，同心圆中的大圆半径为5，小圆半径为3，若大圆的弦AB与小圆有公共点，则AB的最小长度是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 8 |
分析 解决此题首先要弄清楚AB在什么时候最大，什么时候最小．当AB与小圆相切时有一个公共点，此时可知AB最小，由此可以确定AB的最小长度．
解答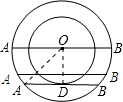 
解：如图，当AB与小圆相切时有一个公共点D，此时AB取最小值，
连接OA，OD，可得OD⊥AB，
∴D为AB的中点，即AD=BD，
在Rt△ADO中，OD=3，OA=5，
∴AD=4，
∴AB=2AD=8，
故选D．
点评 此题考查了切线的性质、勾股定理和垂径定理，知道若大圆的弦AB与小圆有公共点，则AB的最小长度是当AB与圆相切时，是解题的关键．
练习册系列答案
相关题目
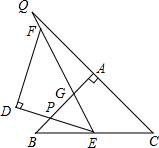如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，射线EF与线段AB相交于点G，与射线CA相交于点Q．若AQ=12，BP=3，则PG=5．
3．有六根细木条，它们的长度分别为3、8、12、15、17、18（单位：cm），从中取出三根首尾顺次连结搭成一个直角三角形，则这三根细木条的长度分别为（ ）
| A． | 3，8，12 | B． | 8，15，17 | C． | 12，15，18 | D． | 3，17，18 |
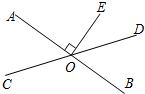如图，直线AB．CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38°，则∠AOC=52 度．
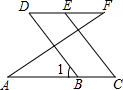如图，已知∠A=∠F，∠C=∠D，按图填空，括号内注明理由