题目内容
6.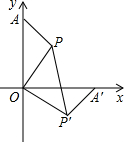 如图所示,在直角坐标系中,点A(0,9),点P(4,6),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则PP′=2$\sqrt{26}$.
如图所示,在直角坐标系中,点A(0,9),点P(4,6),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则PP′=2$\sqrt{26}$.
分析 先根据两点间的距离公式计算出OP=2$\sqrt{13}$,再根据旋转的性质得∠POP′=∠AOA′=90°,OP′=OP,所以△OPP′为等腰直角三角形,则PP′=$\sqrt{2}$OP=2$\sqrt{26}$.
解答 解:∵点P的坐标为(4,6),
∴OP=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∵△AOP绕点O顺时针方向旋转,使OA边落在x轴上,
∴∠POP′=∠AOA′=90°,OP′=OP,
∴△OPP′为等腰直角三角形,
∴PP′=$\sqrt{2}$OP=$\sqrt{2}$×2$\sqrt{13}$=2$\sqrt{26}$.
故答案为2$\sqrt{26}$.
点评 本题考查了坐标与图形变化变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.将一元二次方程x2-2x-2=0配方后所得的方程是( )
| A. | (x-2)2=2 | B. | (x-1)2=2 | C. | (x-1)2=3 | D. | (x-2)2=3 |
17. 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )
 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\sqrt{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | 3cos60°<x<$\frac{{2\sqrt{3}}}{3}$tan60° |
14.自进入秋季以来起,因为天气原因,更多人选择了戴口罩,为了满足市场需求,某厂家生产A、B两种款式的环保口罩,每天共生产500个,两种口罩的成本和售价如下表
若设每天生产A口罩x个.
(1)用含x的代数式表示该工厂每天的生产成本,并进行化简;
(2)用含x的代数式表示该工厂每天获得的利润,并将所列代数式进行化简;(利润=售价-成本)
(3)当x=300时,求每天的生产成本与获得的利润.
| 成本(元/个) | 售价(元/个) | |
| A | 5 | 8 |
| B | 7 | 9 |
(1)用含x的代数式表示该工厂每天的生产成本,并进行化简;
(2)用含x的代数式表示该工厂每天获得的利润,并将所列代数式进行化简;(利润=售价-成本)
(3)当x=300时,求每天的生产成本与获得的利润.
15.下列代数式中,不是单项式的是( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{π}$ | C. | $\frac{1}{x}$ | D. | 3a2b |
 已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.
已知线段AB上顺次有三个点C、D、E,把线段AB分成2:3:4:5四部分,且AB=56cm.