题目内容
 如图,在由相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠BPC=________.
如图,在由相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠BPC=________.

分析:作CH⊥BP于H点,设小正方形的边长为1,根据勾股定理可计算出CD=
 ,AB=
,AB= ,再根据三角形面积公式可计算出CP=
,再根据三角形面积公式可计算出CP= ,然后再利用勾股定理计算出
,然后再利用勾股定理计算出BP=
 ,由BD∥AC得到△BPD∽△APC,利用相似比得到PC=2PD,所以PC=
,由BD∥AC得到△BPD∽△APC,利用相似比得到PC=2PD,所以PC= CD=
CD= ,接着在Rt△PHC中,根据勾股定理计算出PH=
,接着在Rt△PHC中,根据勾股定理计算出PH= ,最后利用正切的定义求解.
,最后利用正切的定义求解.解答:作CH⊥BP于H点,如图,

设小正方形的边长为1,则AC=2,
在Rt△BCD中,CD=
 =
= ,
,在Rt△ABC中,AB=
 =
= ,
,∵
 CP•AB=
CP•AB= BC•AC,
BC•AC,∴CP=
 ,
,在Rt△BPC中,BP=
 =
= ,
,∵BD∥AC,
∴△BPD∽△APC,
∴
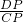 =
=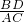 =
= ,即PC=2PD,
,即PC=2PD,∴PC=
 CD=
CD= ,
,在Rt△PHC中,PH=
 =
= ,
,∴tan∠CPB=
 =
= .
.故答案为
 .
.点评:本题考查了相似三角形的判定与性质:有两组角分别相等的两三角形相似;相似三角形的对应角相等,对应边的比相等.也考查了勾股定理和正方形的性质.

练习册系列答案
相关题目

 公平?
公平?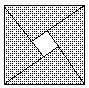
 公平?
公平?