题目内容
13.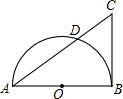 如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.
如图,AB是半圆O的直径,CB是半圆O的切线,B是切点,AC交半圆O于点D,已知CD=1,AD=4,则tan∠CAB=$\frac{1}{2}$.
分析 根据切割线定理可知CB2=CD•CA=5,先求得CB=$\sqrt{5}$;结合Rt△CAB中的条件可求得AB=2$\sqrt{5}$,即可求得tan∠CAB.
解答 解:∵CB2=CD•CA=5,
∴CB=$\sqrt{5}$,
在Rt△CAB中,CB=$\sqrt{5}$,CA=5,根据勾股定理,
AB=2$\sqrt{5}$,
tan∠CAB=$\frac{BC}{AB}$=$\frac{1}{2}$.
点评 本题考查切割线定理和锐角三角函数的定义,在直角三角形中,一个角的正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
13.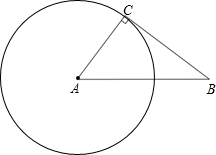 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
 如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )
如图,Rt△ABC中,AB=10cm,BC=8cm,若点C在⊙A上,则⊙A的半径是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
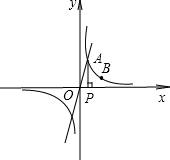 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.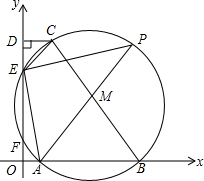 在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.
在平面直角坐标系中,以BC为直径的⊙M交x轴正半轴于点A、B,交y轴正半轴于点E、F,作CD⊥y轴于D连接AM并延长交⊙M于点P,连接PE、AF.